可以看的网站的浏览器有哪些企业网站合同
AMBA总线介绍
系统总线简介
系统芯片中各个模块之间需要要有接口来连接
总线作为子系统之间共享的通信链路
优点:低成本,方便易用
缺点:会造成性能颈瓶
AMBA:Advanced Microcontroller Bus Architecture。片总线的标准
定义了三种总线:AHB(Advanced High-performance Bus)、ASB(Advanced System Bus),APB(Advanced Peripheral Bus)
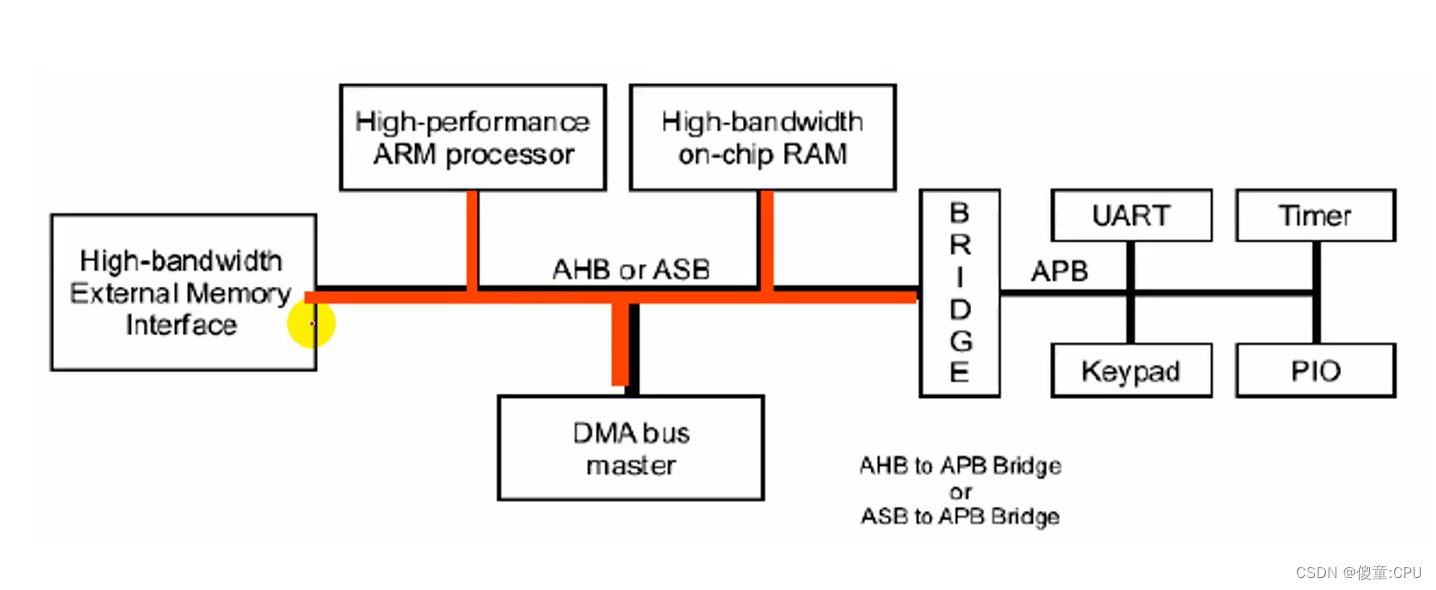
一个典型的AMBA系统
处理器和其他主设备/从设备都是可以替换的
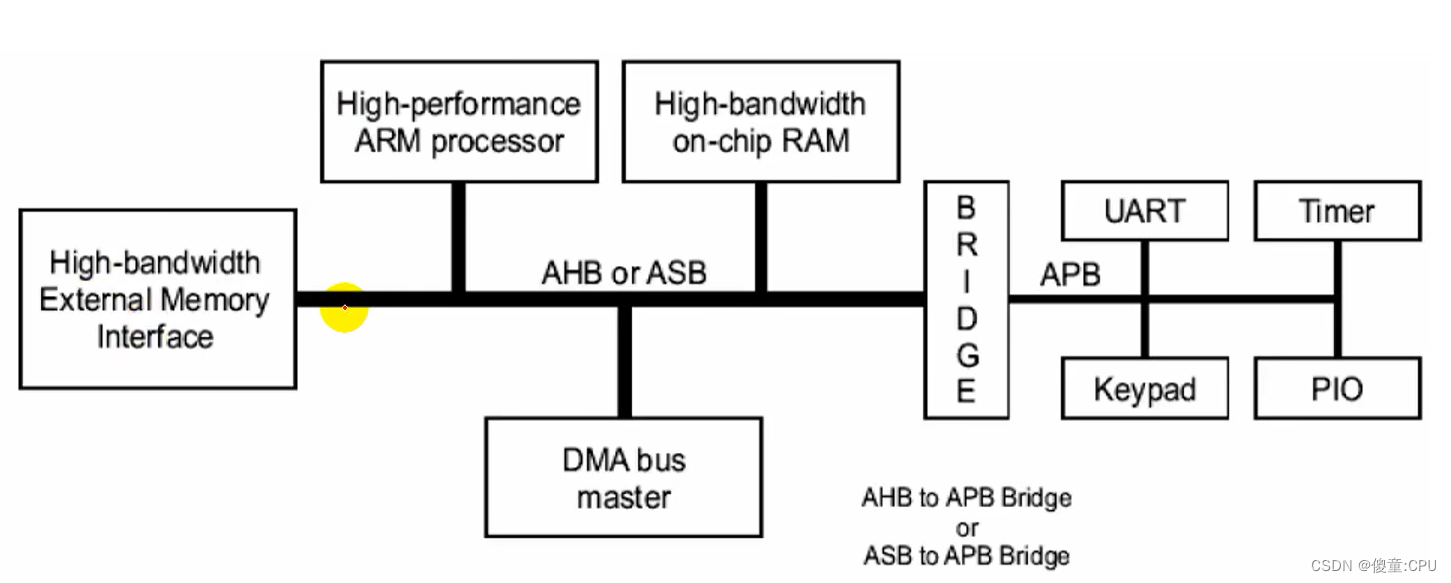
基于AMBA的微控制器典型地由一个高性能系统中枢总线(AMBAAHB或者AMBA ASB)组成,能够支持外部存储器带宽,包括CPU,片上存储器和其他直接数据存取(DMA)设备。这条总线为上述单元之间大多数的传输提供高带宽接口。在这条高性能总线上也有一个桥接器以连接低带宽的APB,而在APB上连接着大多数的系统外设。

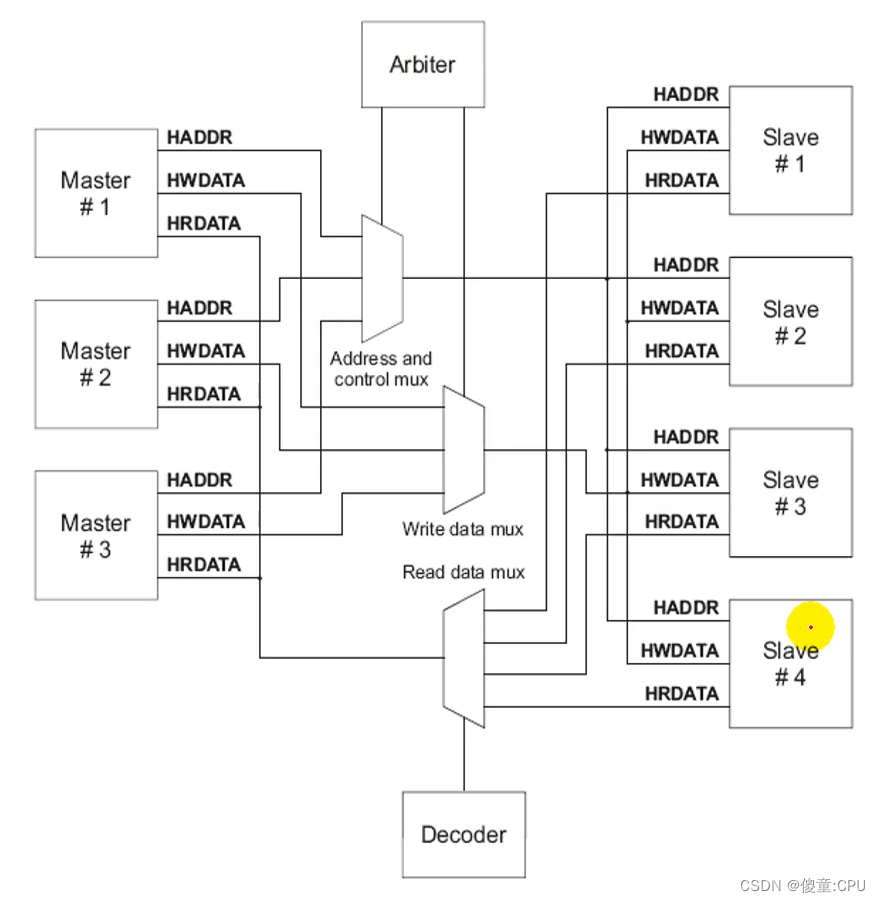
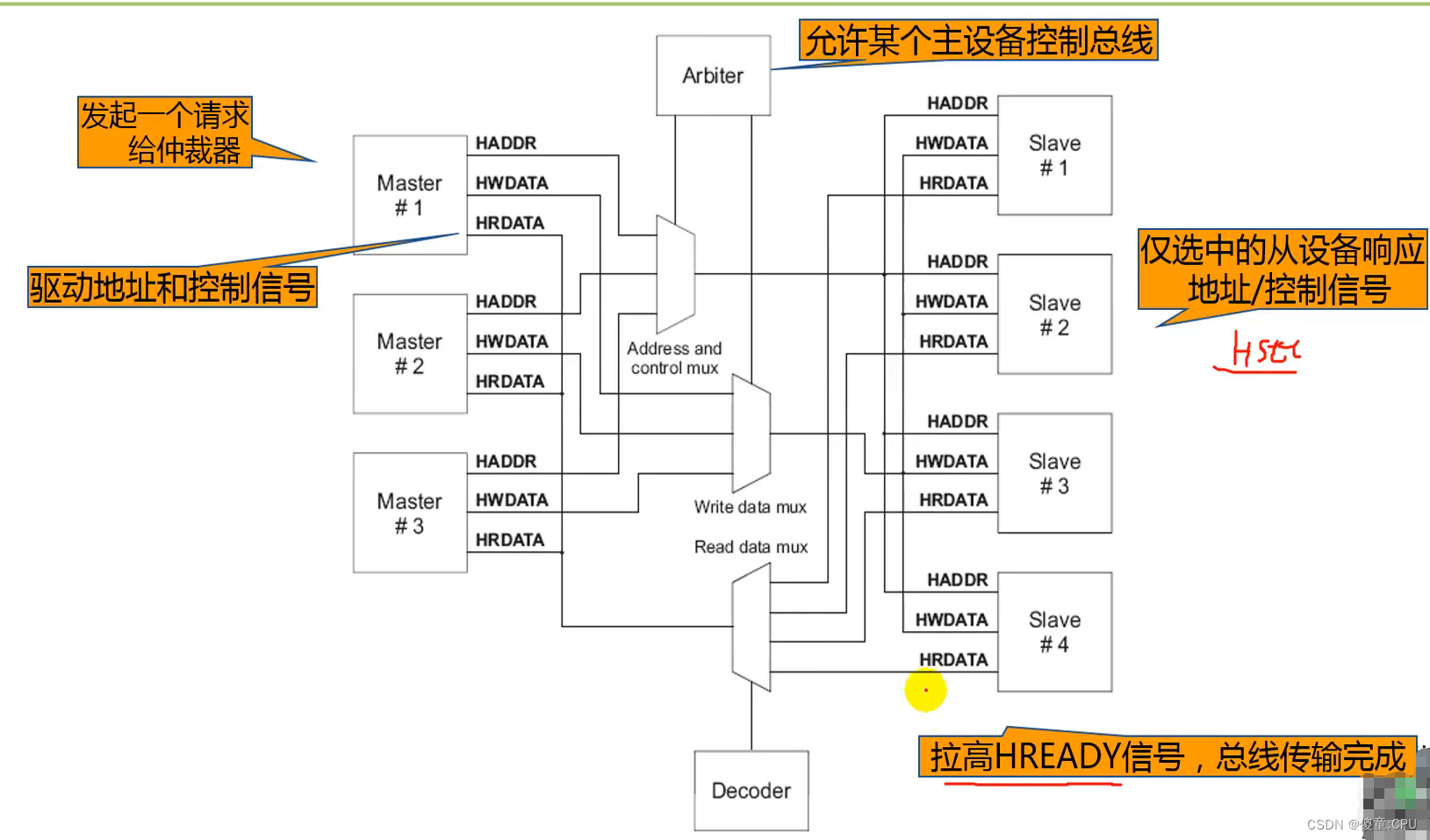
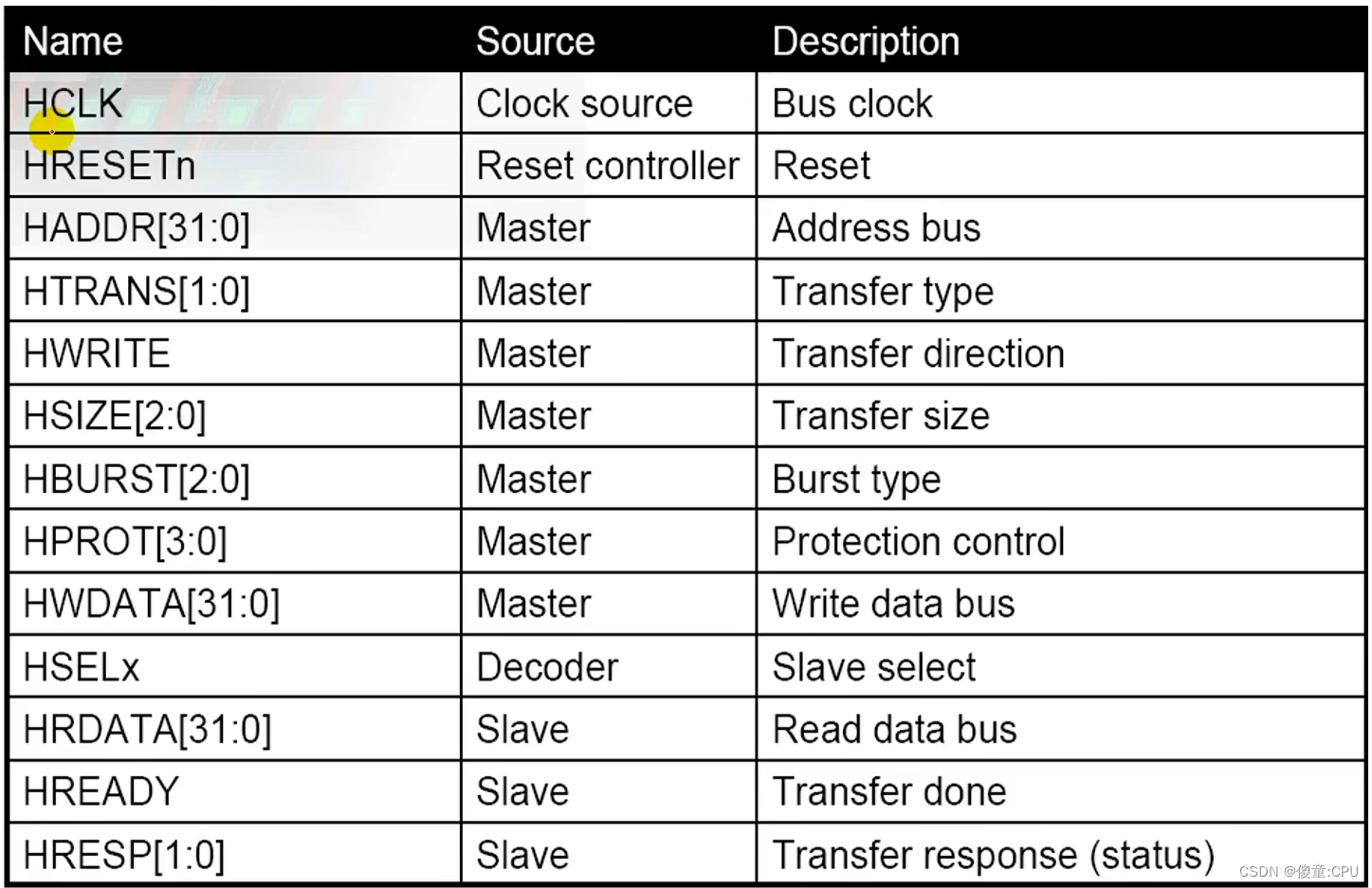
AHB
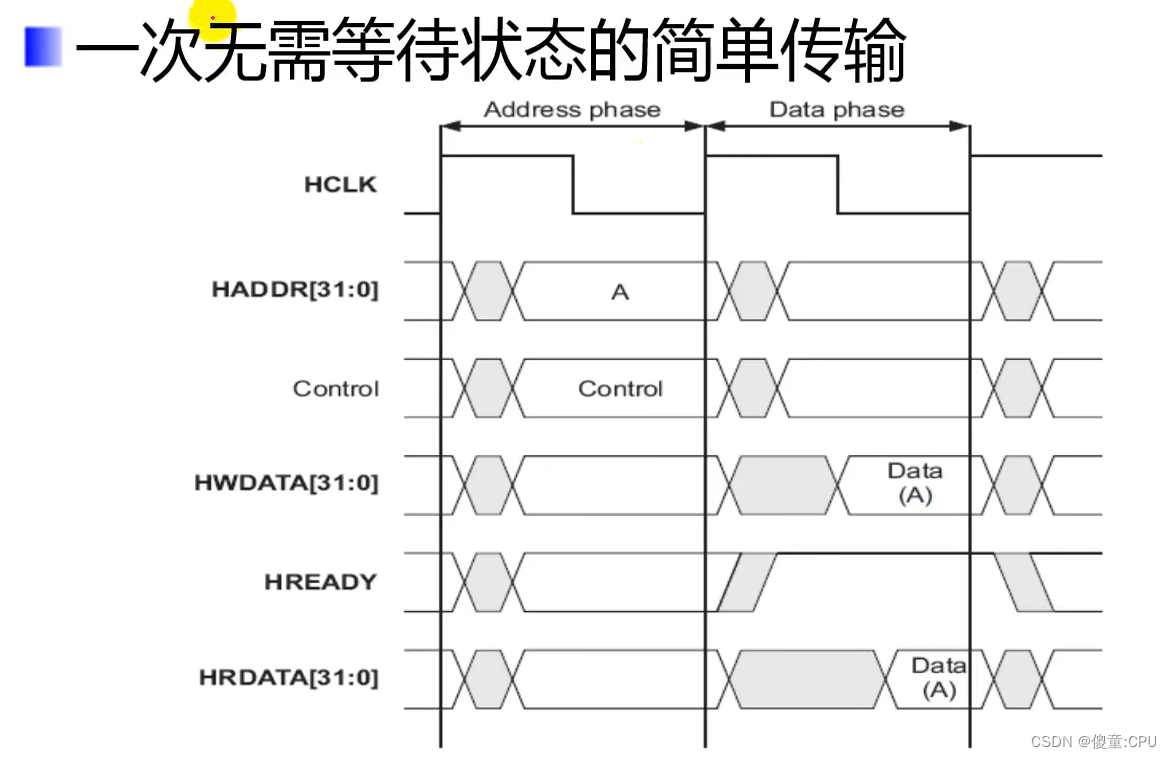
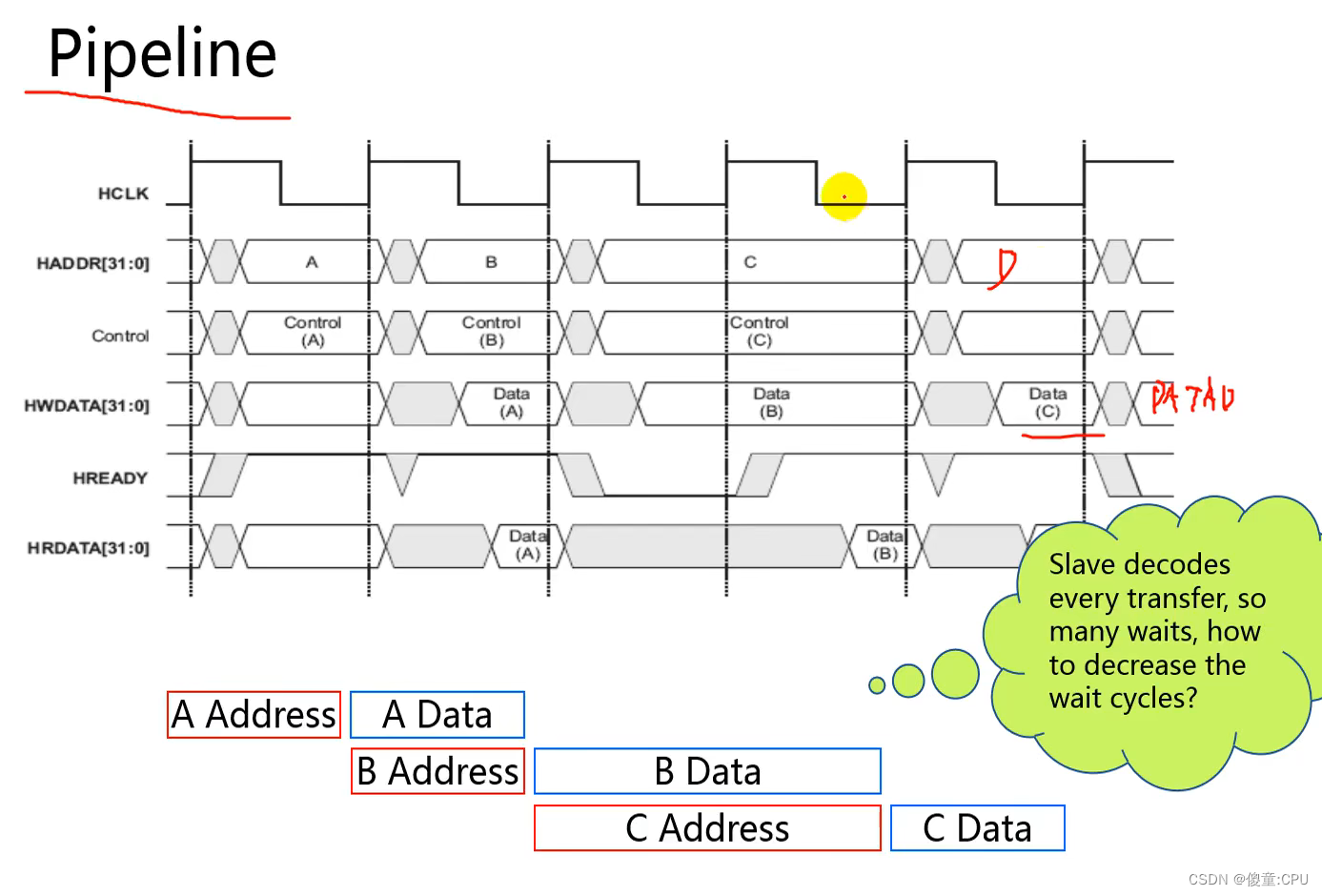
- 高速总线、高性能
- 2级流水线操作
- 可支持多个总线主设备(最多16个)
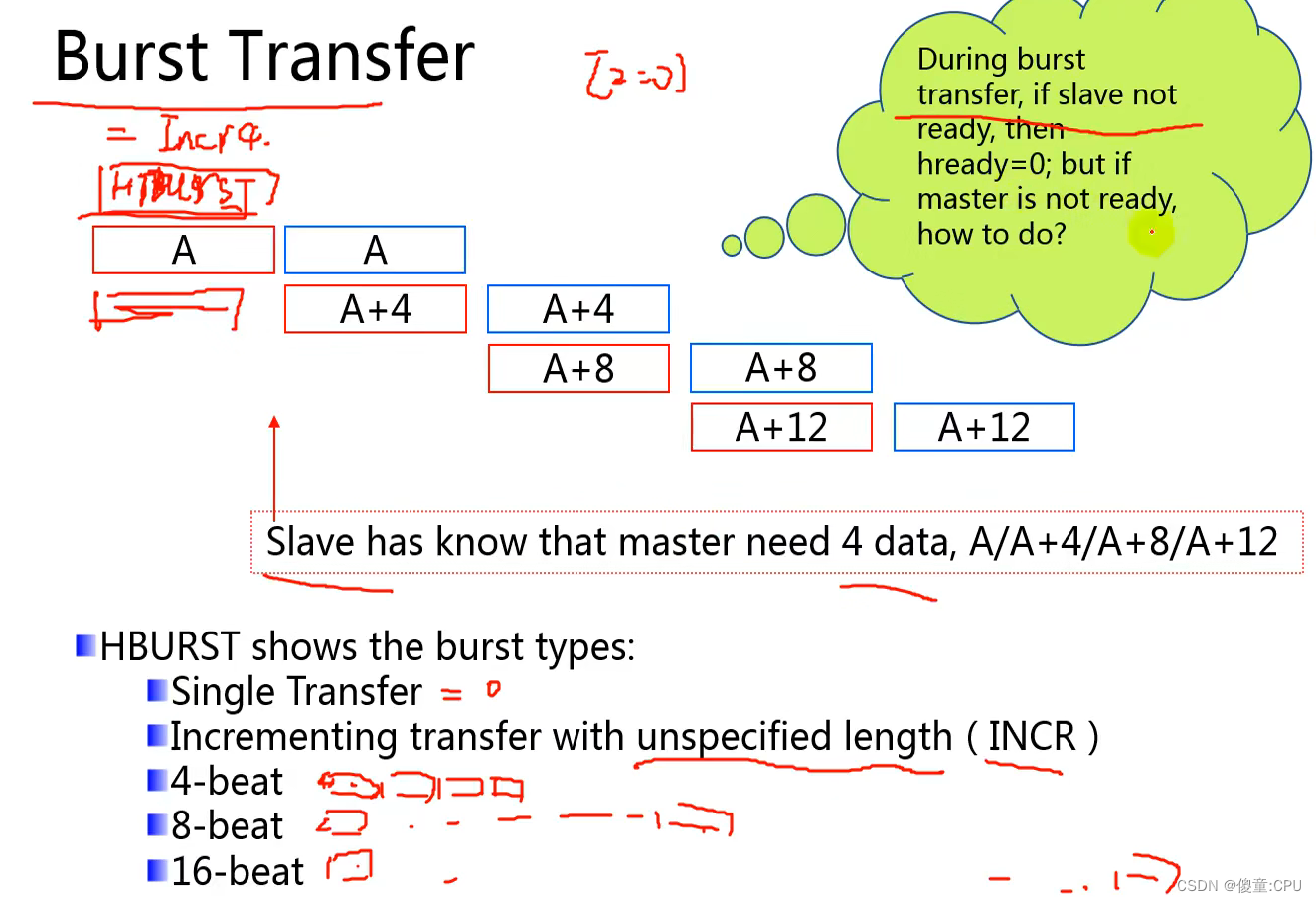
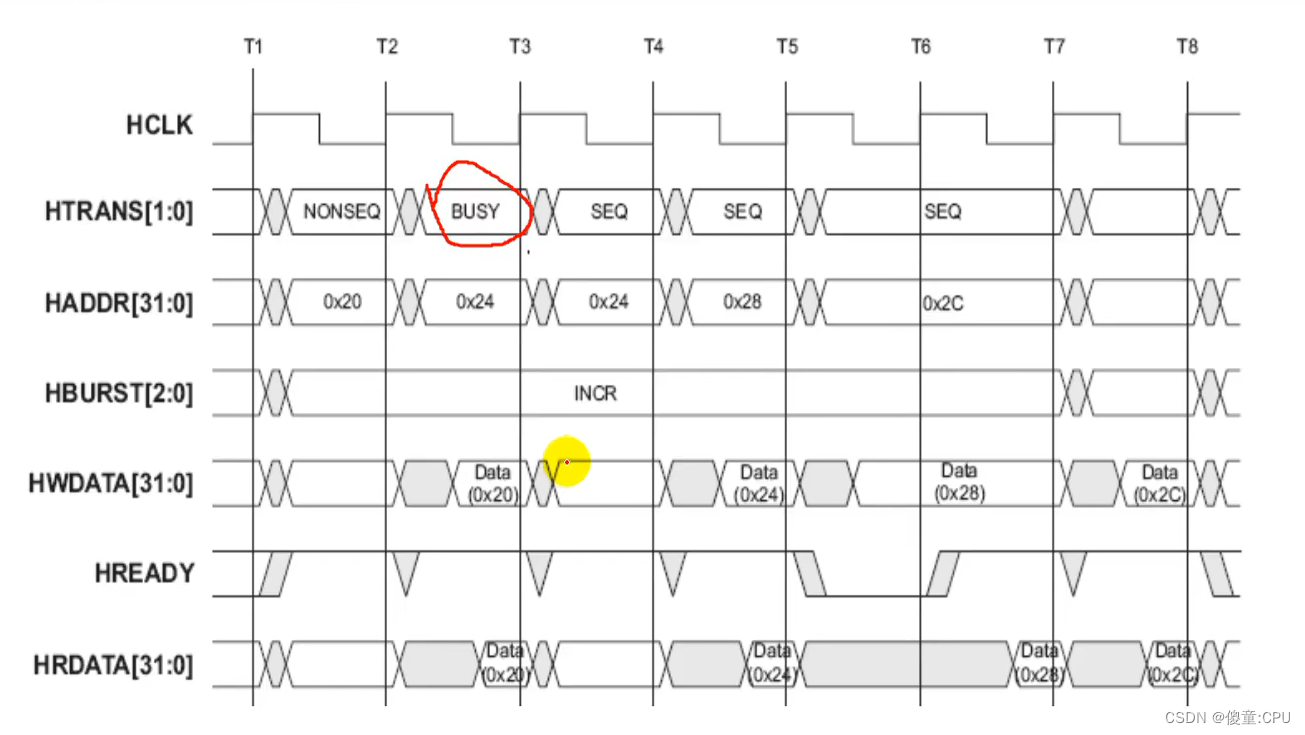
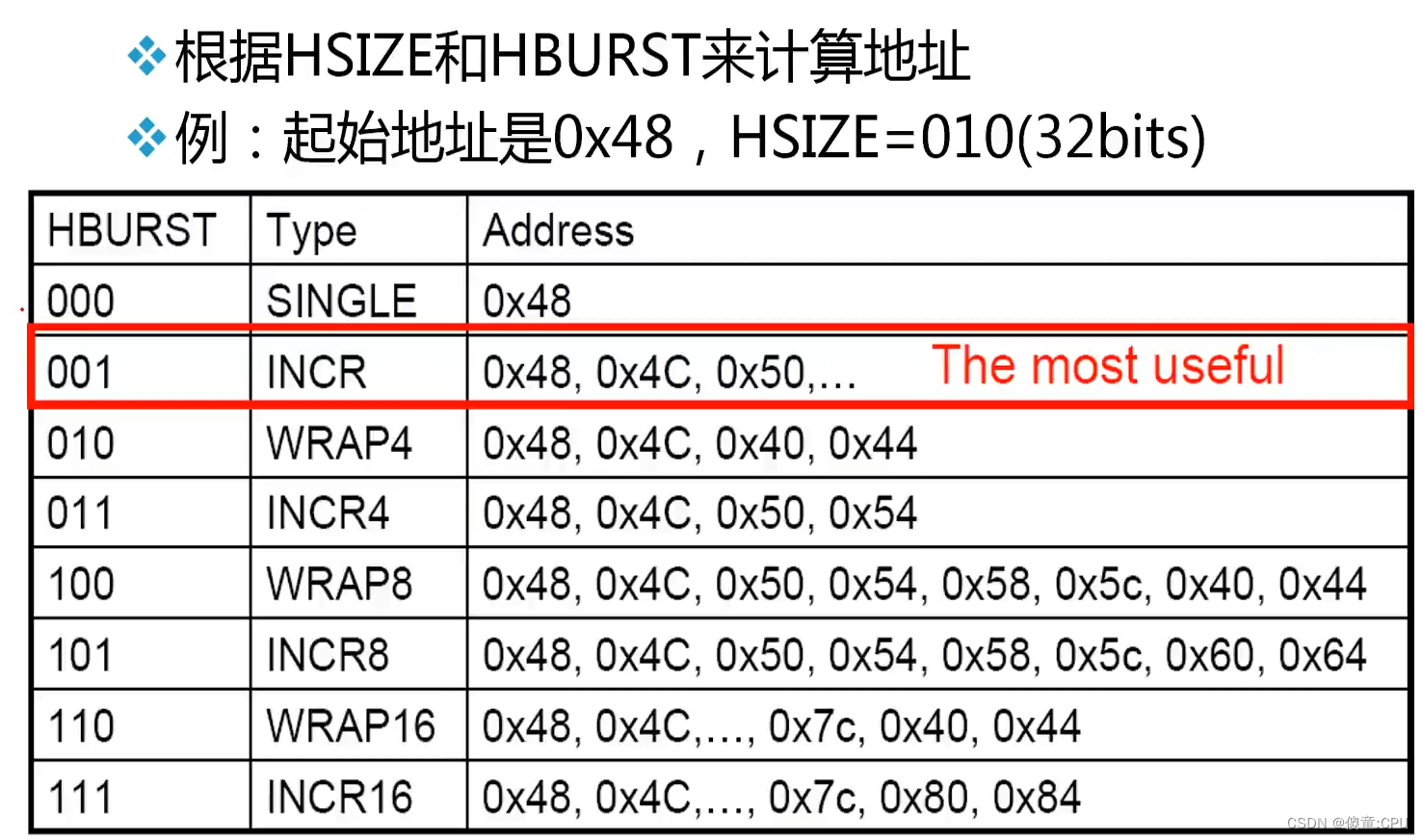
- 支持burst传输 总线带宽:8、16、32、64、128bit
- 上升沿触发操作
- 对于一个新设计建议使用AHB

APB
- 低速总线、低功耗
- 接口简单
- 在Bridge中锁存地址信号和控制信号
- 适用于多种外设
- 上升沿触发

AMBA协议其他有关问题
- 与工艺无关
- 没有定义电气特性
- 仅在时钟周期级定义时序
- 提取时序参数依赖于所采用的工艺和工作频率
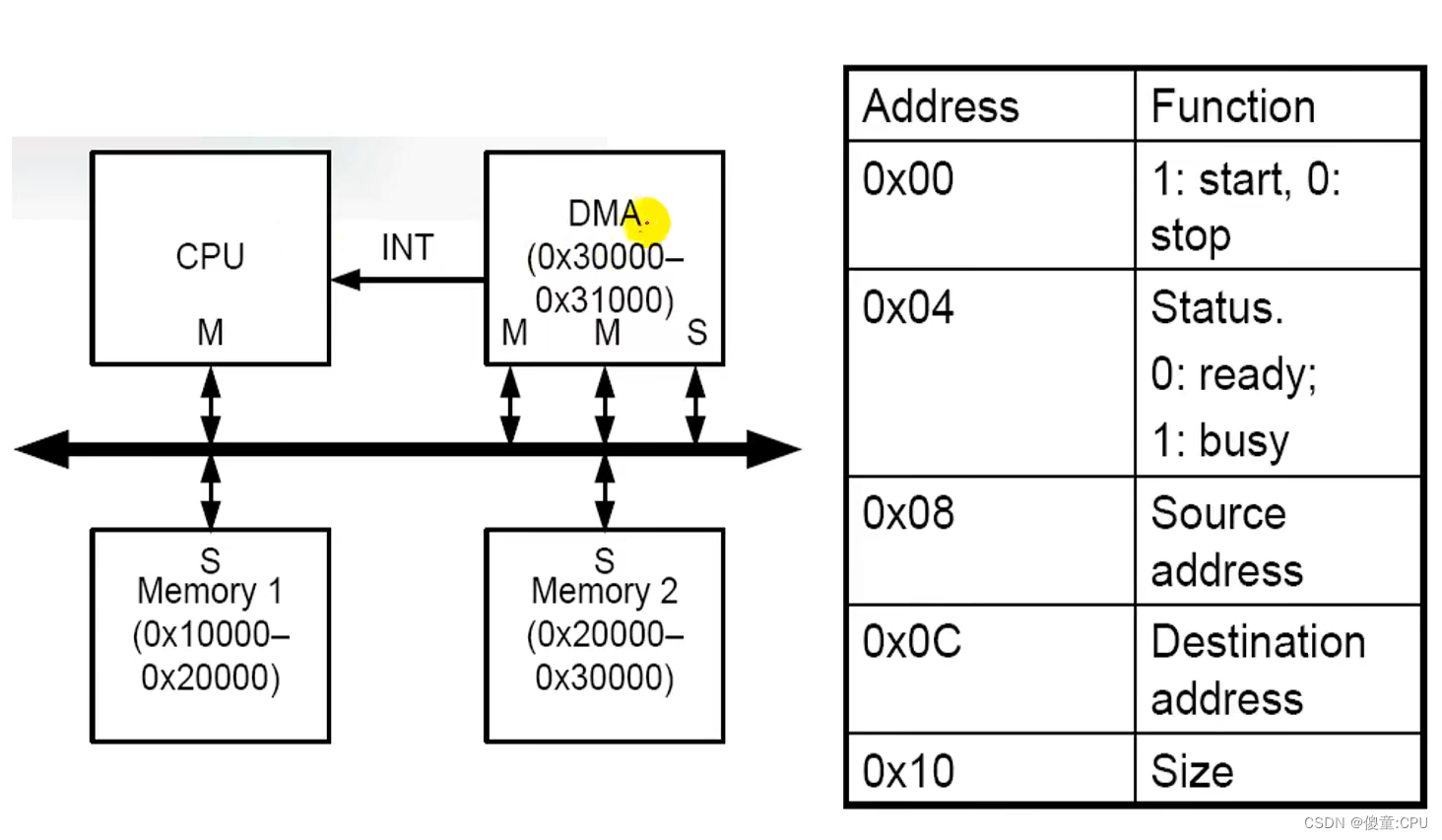
例:DMA
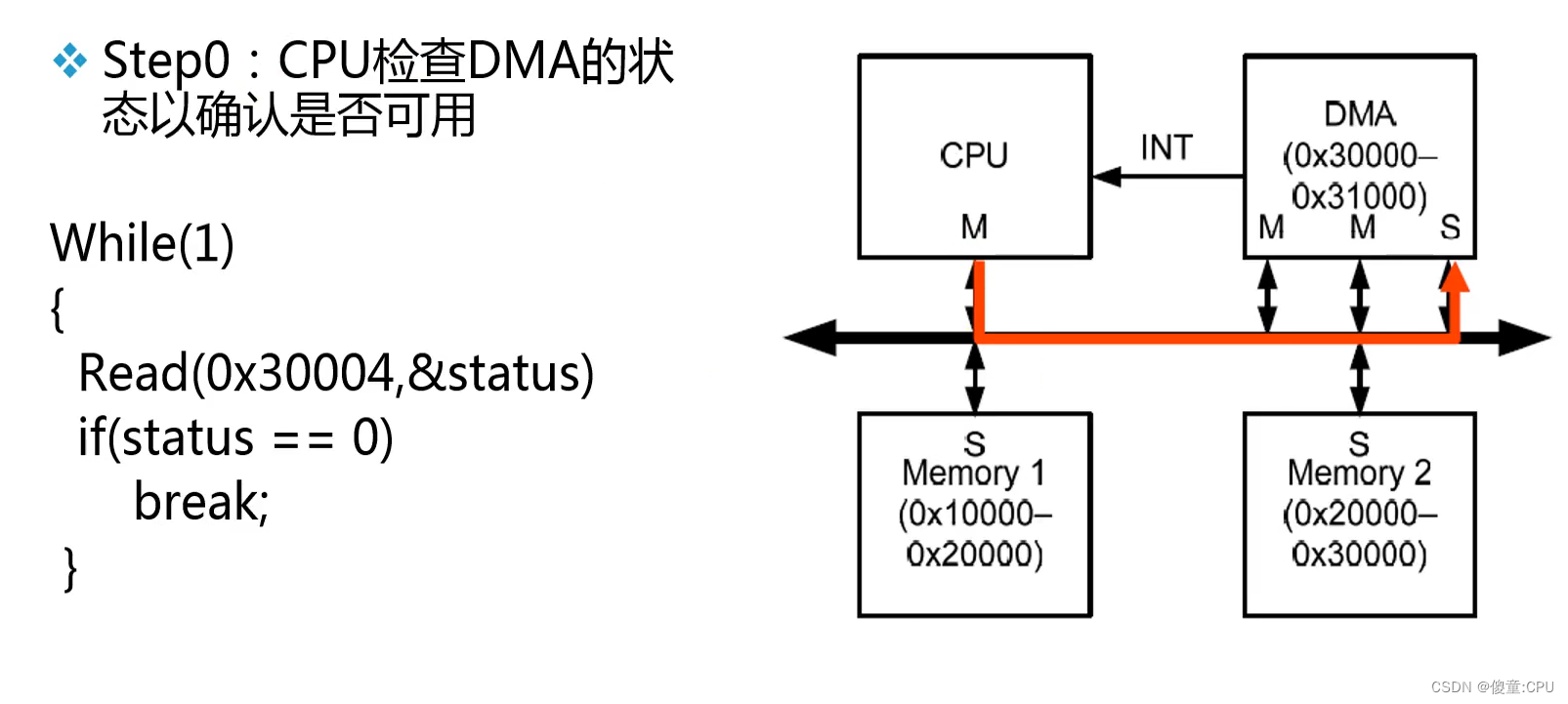
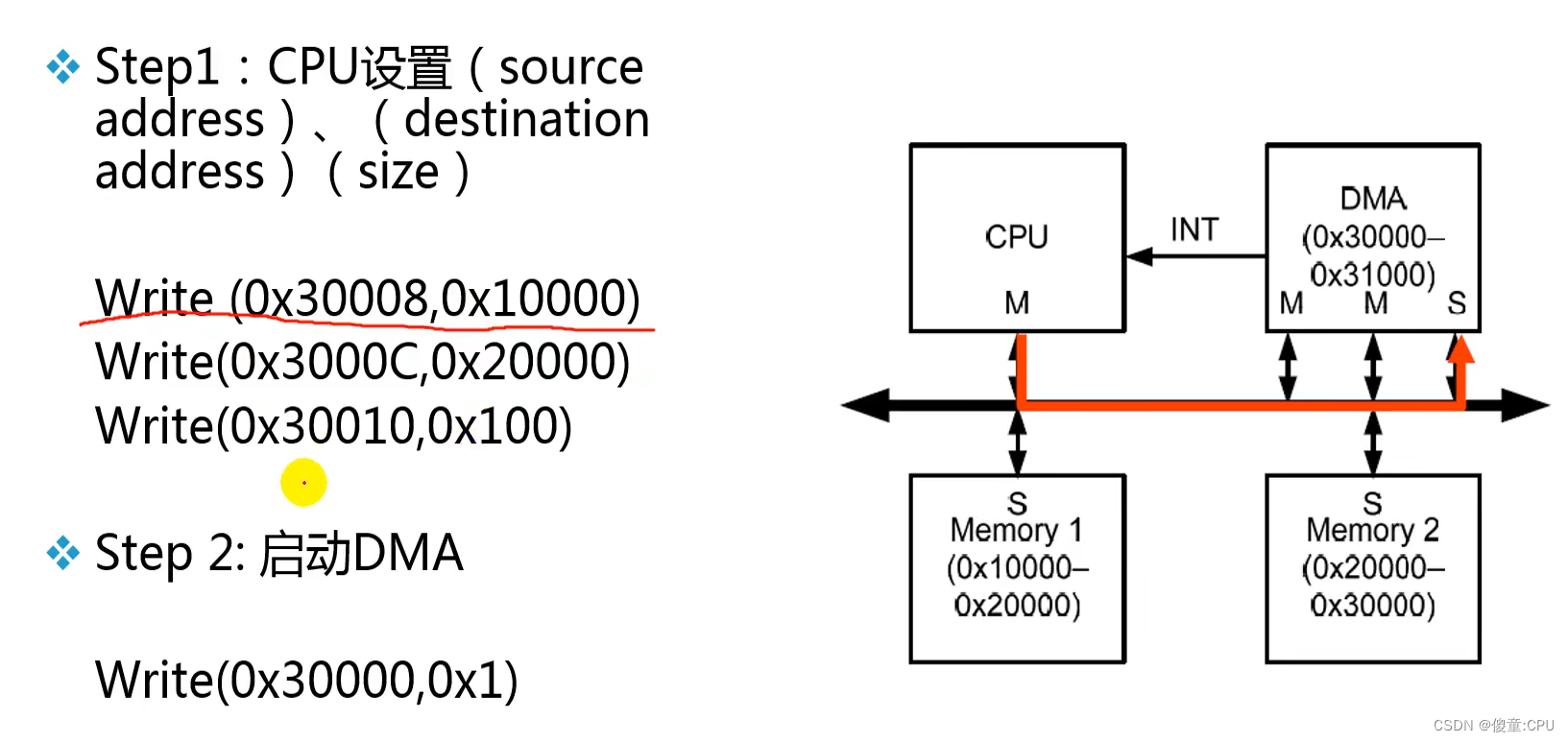
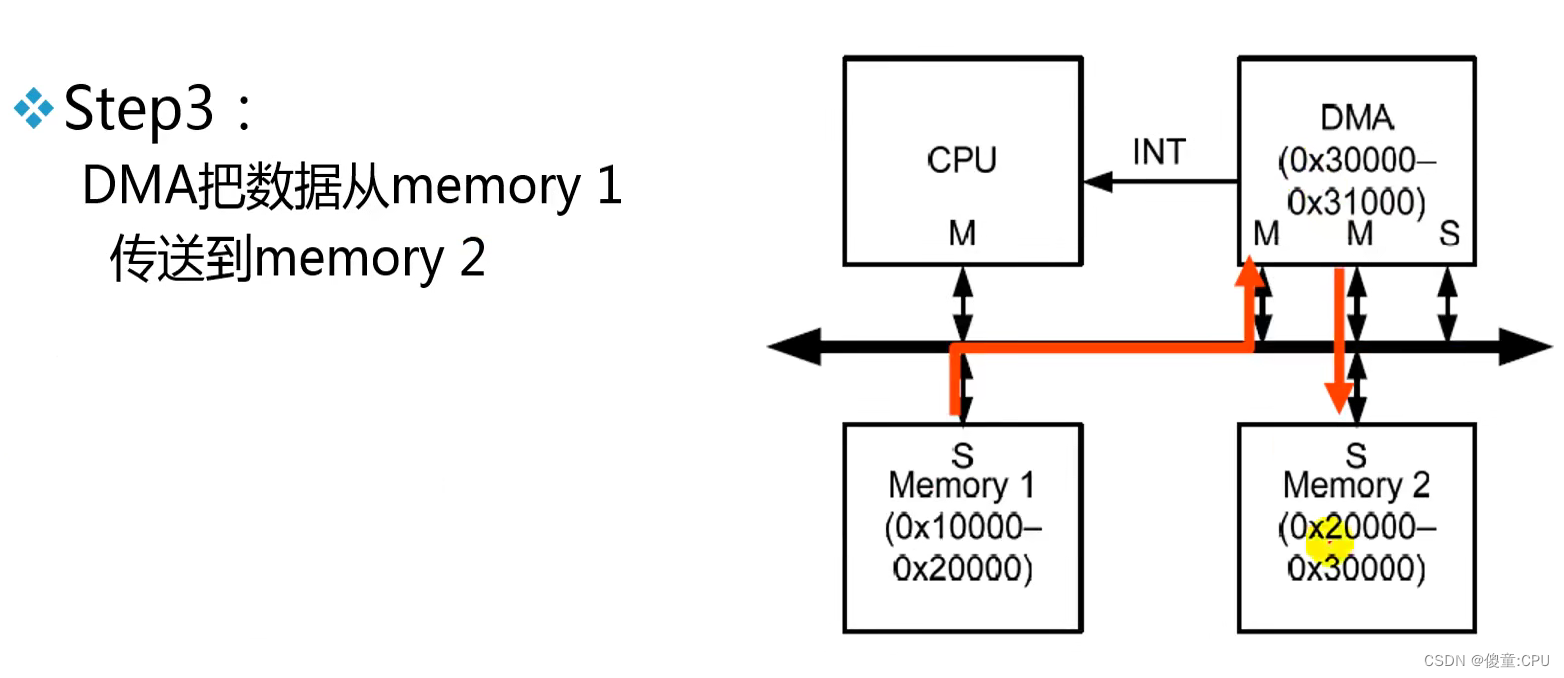
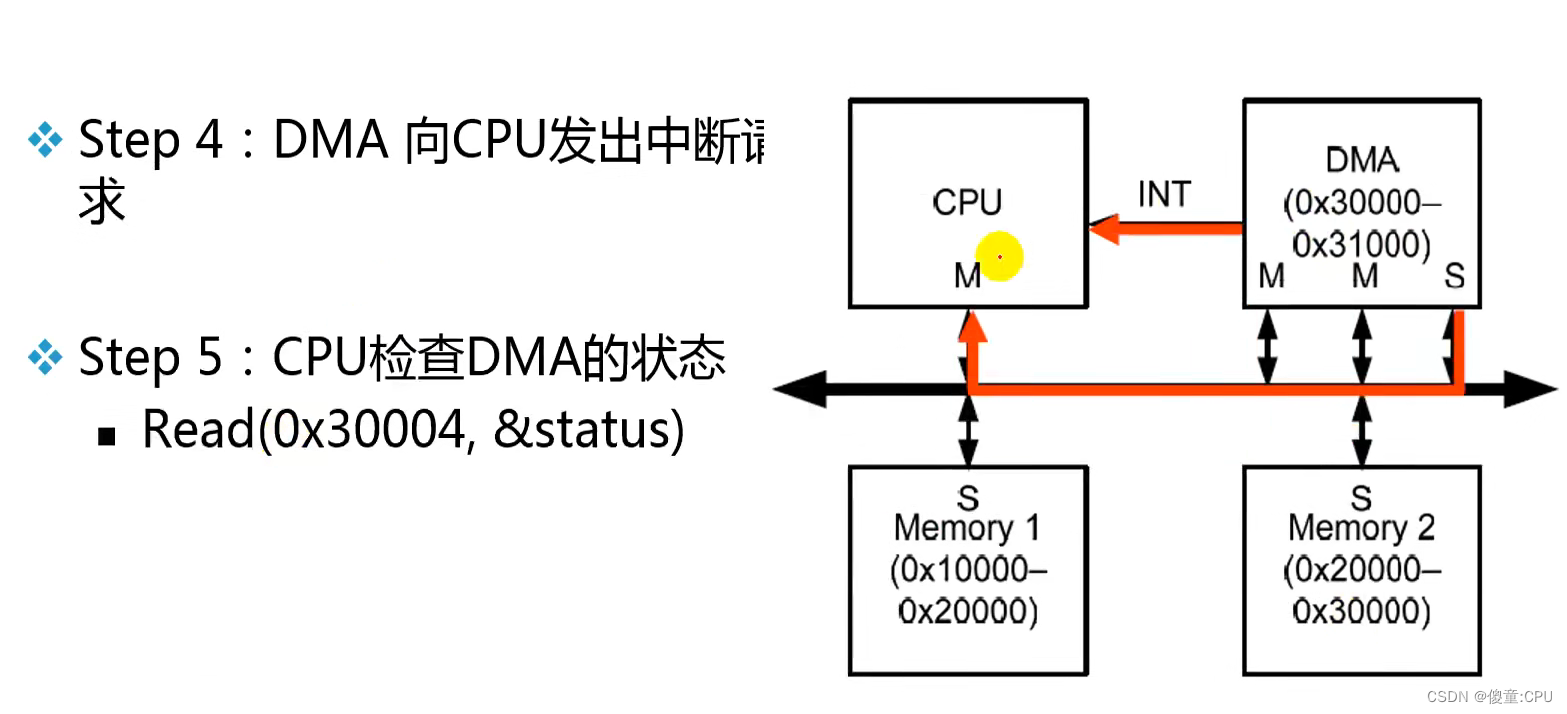
AHB