惠州市+网站开发公司喀什地区建设局网站
前言
大家好,这里是白泽。 《Go语言的100个错误以及如何避免》 是最近朋友推荐我阅读的书籍,我初步浏览之后,大为惊喜。就像这书中第一章的标题说到的:“Go: Simple to learn but hard to master”,整本书通过分析100个错误使用 Go 语言的场景,带你深入理解 Go 语言。
我的愿景是以这套文章,在保持权威性的基础上,脱离对原文的依赖,对这100个场景进行篇幅合适的中文讲解。所涉内容较多,总计约 8w 字,这是该系列的第一篇文章,对应书中第1-10个错误场景。
🌟 当然,如果您是一位 Go 学习的新手,您可以在我开源的学习仓库中,找到针对 《Go 程序设计语言》 英文书籍的配套笔记,期待您的 star。
公众号【白泽talk】,聊天交流群:622383022,原书电子版可以加群获取。
1. Go: Simple to learn but hard to master
🌟 章节概述:
- 为什么 Go 高效、可扩展、富有生产力
- 为什么说 Go 易学难精
- 介绍开发者常犯的几种类型的错误
1.1 Go 语言概述
- 稳定:更新频繁,但核心功能稳定
- 表现力:用少的关键词解决更多的问题
- 编译:快速编译提高生产力
- 安全:严格的编译时规则,确保类型安全
Go 语言层面通过 goroutines 和 channels 提供了出色的并发编程机制,无需像其他语言一样使用第三方高性能的库,本身就具备高性能,战未来!
一位大厂的前辈留下的五字箴言:
1.2 简单不等于容易
简单:易于理解,方便学习(鄙视链大概是从这里来的)
容易:不怎么努力就可以全面掌握(这一点每一个语言都是如此)
书中这部分举例开源项目 docker、grpc、k8s 论证使用 channel 在 goroutines 间传递 message,经常编码失误导致问题。因为 goroutines 间是并发运行的,执行顺序无法预测。区别于纯流程式的编程,将解决一个问题分成 n 个步骤,然后依次编码,依次调用其他函数,按序执行。
为了发挥 Go 的并发支持能力,知名 Go 项目中大量使用 goroutines & channels 用作控制程序的执行顺序,而不仅仅是代码编写的顺序决定执行顺序。当各种日志、状态、消息需要在你的程序中传递,那免不了需要仔细编排 message 的流转和流程控制。
毕竟,我们都知道解决并发问题的的最好办法:不用并发。 使用 Go 可以不用 channel,甚至不用除了主协程之外的 goroutines,那一定十分安全,但这违背了使用 Go 语言的初衷,也就无法发挥它的能力。
🌟 总结:Go 的高性能是建立在合理的编码之上的。给你独步天下的招式,但也需要你修炼内功,简单不等于容易。
1.3 使用 Go 的100个错误
因人为使用不当造成的,使用 Go 的100个错误场景可以分成以下几种类型,:
- Bug
- 不必要的复杂性
- 代码可读性差
- 代码组织结构差
- 提供的 API 用户不友好
- 编码优化程度不够
- 使用 Go 编程但生产力低下
通过对错误使用场景的分析,可以有针对性的加深我们对 Go 语言的理解,让我们开始吧。
🌟 所有标题中使用#number的形式,标明这是第几个错误场景
2. Code and project organization
🌟 章节概述:
- 主流的代码组织方式
- 高效的抽象:接口和范型
- 构建项目的最佳实践
2.1 变量屏蔽(#1)
Go 语言当中,在一个块作用域中声明的变量,可以在更内部的块中被重新声明。
错误示例:
var client *http.Client
if tracing {client, err := createClientWithTracing()if err != nil {return err}log.Println(client)
} else {client, err := createDefaultClient()if err != nil {return err}log.Println(client)
}
// 使用 client
client 在内部块中被重新声明,并使用,并不改变外部的 client 的值,所以外部 client 始终为 nil,且由于外部 client 在下文被使用,编译时不会报 “client declared and not used”的错误。
修正方案:
var client *http.Client
var err error
if tracing {client, err = createClientWithTracing()
} else {client, err = createDefaultClient()
}
if err != nil {// 处理 err
}
// 使用 client
短变量声明符号 := 会重新声明变量,这里替换成赋值操作,并统一处理 err。
2.2 没有必要的代码嵌套(#2)
错误示例:
func join(s1, s2 string, max int) (string, error) {if s1 == "" {return "", errors.New("s1 is empty")} else {if s2 == "" {return "", errors.New("s2 is empty")} else {concat, err := concatenate(s1, s2)if err != nil {return "", err} else {if len(concat) > max {return concat[:max], nil} else {return concat, nil}}}}
}
func concatenate(s1, s2 string) (string, error) {// ...
}
由于复杂的嵌套导致无法直观阅读所有的 case 的执行流程。
修正方案:
func join(s1, s2 string, max int) (string, error) {if s1 == "" {return "", errors.New("s1 is empty")}if s2 == "" {return "", errors.New("s2 is empty")}concat, err := concatenate(s1, s2)if err != nil {return "", err}if len(concat) > max {return concat[:max], nil}return concat, nil
}
func concatenate(s1, s2 string) (string, error) {// ...
}
减少 if 之后没有必要的 else 嵌套,使得所有 case 可以一眼明了。
🌟 书中用 happy path 这个概念,表示决定程序执行流程的不同逻辑判断代码。
修正方案中将 happy path 全部放在靠左侧的第一层,使得代码的阅读性很好。
2.3 误用 init 函数(#3)
概念介绍:
init 函数用于初始化应用的状态,但不可以被直接调用。
当一个 package 被初始化的时候,所有的定义的常量和变量先初始化,再执行 init 函数。如果依赖了其他 package 的代码,则先初始化依赖方。这个顺序再多层依赖的时候可以继续推广。
而同一个 package 中的 init 函数按照字典序调用。但不要依赖这种顺序,这没有意义。
调用示例:
package main
import ("redis"
)
// 3️⃣
var a = 1
// 4️⃣
func init() {// ...
}
// 5️⃣
func main() {err := redis.Store("foo", "bar")// ...
}
-------------------------------------------------
package redis
// 1️⃣
var b = 2
// 2️⃣
func init() {// ...
}
func Store(key, value string) error {// ...
}
解释:包 B 被导入包 A 时,包 B 的包级别变量(var)会先初始化,然后调用包 B 中的 init 函数。接着,导入包 A 的包级别变量会初始化,最后调用包 A 中的 init 函数。
错误示例:
var db *sql.DB
func init() {dataSourceName := os.Getenv("MYSQL_DATA_SOURCE_NAME")d, err := sql.Open("mysql", dataSourceName)if err != nil {log.Panic(err)}err = d.Ping()if err != nil {log.Panic(err)}db = d
}
上述代码的三个缺点:
-
init 函数中错误处理受限,一旦出错会 panic,不允许这个 package 的调用者手动处理错误逻辑。
-
为这个文件写单测的时候,即使测试其他函数,init 函数也会被调用,使得单测流程复杂化。
-
将数据库连接赋值给全局变量会导致问题:
- 任何函数可以对其进行修改。
- 依赖了全局变量,单测运行会更复杂,因为它变得不再隔离。
修正方案:
func createClient(dsn string) (*sql.DB, error) {db, err := sql.Open("mysql", dsn)if err != nil {return nil, err}if err = db.Ping(); err != nil {return nil, err}return db, nil
}
🌟 在你的使用场景中,如果能够避免上面提到的三个 issue,则可以使用 init 函数。但绝大多数情况下,还是推荐修正方案的写法。
2.4 过度使用 getter & setter(#4)
Go 语言并不强制使用 getter 和 setter 方法去设置值。
Go 的标准库 time 使用示例:
timer := time.NewTimer(time.Second)
<-time.C
我们甚至可以直接修改 C,尽管这十分不推荐。因此为了确保 Go 语言的简单性,getter & setter 的使用需要自行把握。封装是有好处的,但使用时确保它对你的程序是有价值的再开始使用。
推荐命名:
currentBalance := customer.Balance() // 不使用 GetBalance 命名
if currentBalance < 0 {customer.SetBalance(0) // 使用 SetBalance 命名
}
2.5 接口污染(#5)
interface 介绍:
使用接口声明可以被多个对象实现的行为(方法),但与其他语言不同,Go 对接口的实现是隐式的,没有类似 implements 这样的关键词。
io 标准库定义的接口以及使用示例:
package io
type Reader interface {Read(p []byte) (n int, err error)
}
type Writer interface {Write(p []byte) (n int, err error)
}
---------------------------------------------------------
func copySourceToDest(source io.Reader, dest io.Writer) error {// ...
}
func TestCopySourceToDest(t *testing.T) {const input = "foo"source := strings.NewReader(input)dest := bytes.NewBuffer(make([]byte, 0))err := copySourceToDest(source, dest)if err != nil {t.FailNow()}got := dest.String()if got != input {t.Errorf("expected: %s, got %s", input, got)}
}
接口中方法越多,抽象程度越低。
🌟 使用 interface 的三个出发点:
- 声明通用的行为
sort 标准库中针对所有基于索引的集合的排序接口:
type Interface interface {Len() intLess(i, j int) boolSwap(i, j int)
}
有了这个排序的接口,则可以针对它进行各种排序函数的实现:快速排序、归并排序…
- 依赖解耦
以一个顾客存储服务为例,举两个例子进行对比,说明使用 interface 解耦的好处。
使用具体类型:
type CustomerService struct {store mysql.Store // 具体的存储实现
}
func (cs CustomerService) CreateNewCustomer(id string) error {customer := Customer{id: id}return cs.store.StoreCustomer(customer)
}
使用 interface 解耦:
type customerStorer interface {StoreCustomer(Customer) error
}
type CustomerService struct {storer customerStorer // 定义存储的接口
}
func (cs CustomerService) CreateNewCustomer(id string) error {customer := Customer{id: id}return cs.storer.StoreCustomer(customer)
}
🌟 好处:
- 集成测试时可以使用不同的 store 依赖源(之前必须依赖 mysql 做集成测试)。
- 可以使用 mock 进行单元测试。
- 约束行为
type IntConfig struct {
}
func (c *IntConfig) Get() int {return 0
}
func (c *IntConfig) Set(value int) {
}
type intConfigGetter interface {Get() int
}
type Foo struct {threshold intConfigGetter
}
func newFoo(threshold intConfigGetter) Foo {return Foo{threshold: threshold,}
}
func main() {c := &IntConfig{}f := newFoo(c)fmt.Println(f.threshold.Get())
}
通过接口限制,即使工厂方法 newFoo 传入的是实现两个接口的 IntConfig 实例,但是 f.threshold 只能够调用 Get 方法。因为 threshold 字段是 intConfigGetter 定义的接口。
🌟 接口污染
很多 Java 或者 C# 转换过来的用户,在创建具体类型前自然而然先创建 interface,这在 Go 当中是不必要的。使用 interface 需要遵循上述的三个出发点(声明通用行为、约束行为、解耦依赖) ,并在需要的时候使用,并获得收益。而不是在当下去预见未来可能需要使用的时,就在此刻声明好 interface,这只会使代码更加难以阅读。
滥用 interface 会使代码难以阅读,因为多增加了一层理解成本。抽象场景应该从业务中被发现被提取,而不是被创造。
2.6 在生产侧的接口(#6)
生产侧:接口与其实现方定义在同一个 package 中。
消费侧:接口定义在相对其实现方的外部的 package 中。
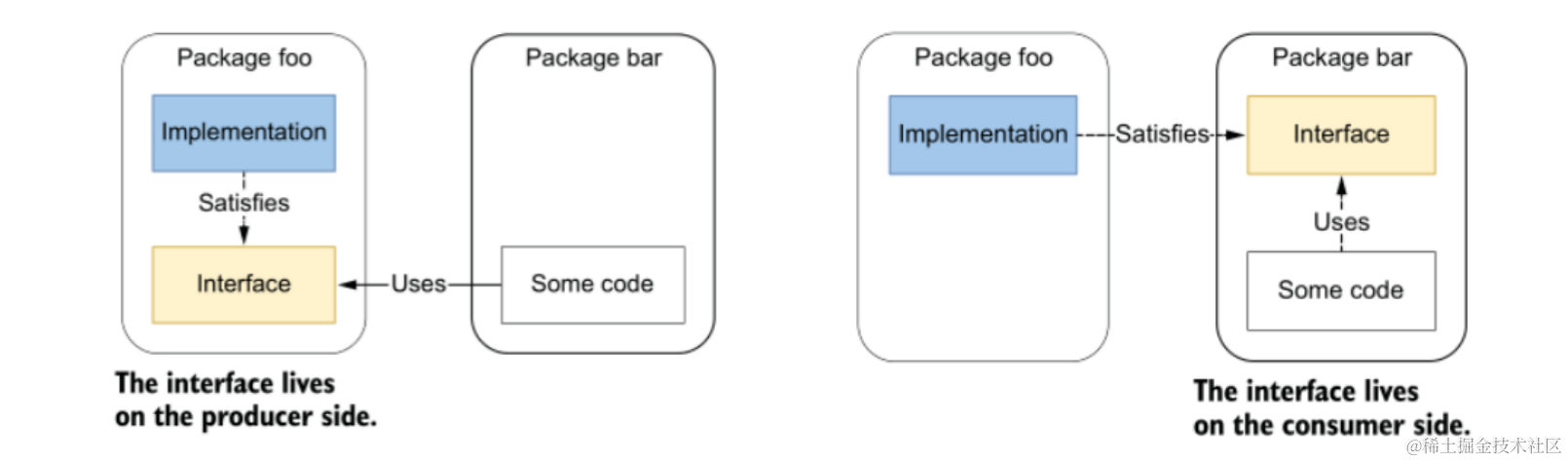
在生产侧声明接口,并为其提供实现,这种方式是 C# 或 Java 开发者的习惯,但在 Go 当中,不应该这么做。(其隐式的接口实现机制,也是为了开发者灵活选择接口的实现方式)
举个例子,假设生产侧的一个顾客存储服务通过接口声明了其所有行为:
package store
type CustomerStorage interface {StoreCustomer(customer Customer) errorGetCustomer(id string) (Customer, error)UpdateCustomer(customer Customer) errorGetAllCustomers() ([]Customer, error)// ...
}
// 一个针对 CustomerStorage 接口的实现
但在消费端开发者使用的时候,可以结合情况对其进一步进行解耦,因为并不一定会用到这个 CustomerStorage 接口定义的所有方法,比如只声明获取所有顾客的方法。
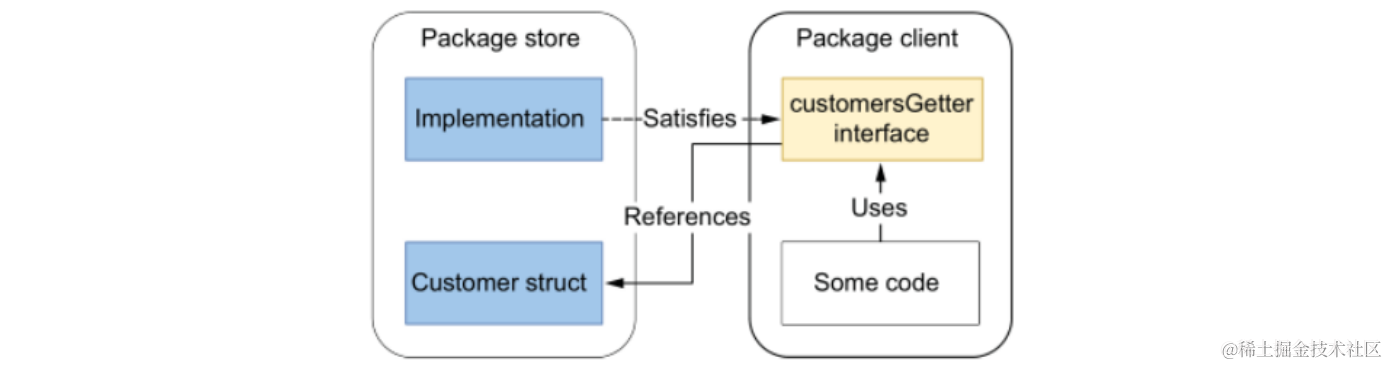
package client
type customerGetter interface {GetAllCustomers() ([]Customer, error)
}
此时 client 包中的 customerGetter 接口在设计时参考了 store 包中的 CustomerStorage 接口,确保 GetAllCustomers 方法的函数签名相同。使得 store 包中的实现类依旧满足 client 包中新声明的 customerGetter 接口,且它被约束后只能调用这一个方法。
⚠️ 注意点:
- customerGetter 接口是参考 store 接口编写的,只服务于 client 包,因此小写开头,不可导出。
- 生产侧 store 包中预先的实现类实现了 client 包中新声明的接口,但由于是隐式实现,没有循环引用的问题。
🌟 生产侧接口使用最佳实践:在生产侧定义接口,并提供实现。而在消费端使用时,需要结合实际情况,考虑是否要引入新接口,选择需要的实现。(事实上)
🌟 生产侧接口定义的方法通常使用在标准库或者为第三方提供支持的 package 当中,设计时需要结合实际,确保一切预先定义的行为都是有意义的。(毕竟 interface 应该在使用是被发现,而不是一开始被创造)
2.7 返回接口(#7)
Go 当中,返回接口类型而不是 struct 是一种不好的设计,错误示例:
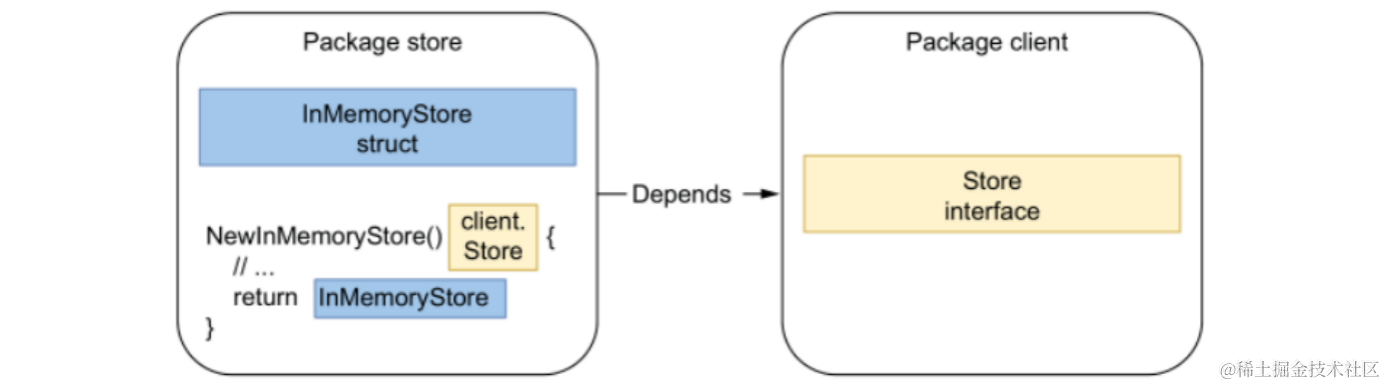
InMemoryStore 结构实现了 client 包的 Store 接口,在调用 NewInMemoryStore 方法的时候返回接口类型。
缺陷:
- client 包将无法再调用 store 包的内容,因为有循环依赖。
- 这使得 store 这个包强依赖了 client 这个包。如果另一个包 tmp 需要使用 store 中的内容,它就会和 client 包也绑定在一起,复杂度极具上升,或许可以尝试修改,改变 Store 接口的位置,但这些复杂度并不应该一开始就存在。
🌟 设计哲学:对自己做的事保持保守,开放接受他人做的事。
反映出的最佳实践:
- 返回结构体而不是接口
- 如果可以,接受接口作为参数
🌟 反例:
很多函数都会返回 error 类型,它本身就是一个接口,此外标准库中也有返回接口类型的情景(如下)。但这些场景都是预先设计且确保收益显著才打破的上述最佳实践规则。
package io
// io.Reader 是一个接口
func LimitReader(r Reader, n int64) Reader {return &LimitReader{r, n}
}
2.8 any 以偏概全(#8)
Go 当中,interface{} 类型表示空接口,即没有声明方法的一个接口,因此可以表示 Go 内部所有的对象。从 Go1.18 开始,引入 any 关键字作为空接口的别名,所有 interface{} 可以用 any 替代。
使用 any 丢失了所有的类型信息,放弃了 Go 作为静态编译语言的优势,相关信息必须再通过断言去提取。
package store
type Customer struct {// ...
}
type Contract struct {// ...
}
type Store struct {}
func (s *Store) Get(id string) (any, error){// ...
}
func (s *Store) Set(id string, v any) error {// ...
}
这段代码通过 Get 和 Set 可以将不同 struct 存入 Store 结构,但调用 Get 后无法直观判断的到的是什么类型,同时 Set 的时候,也没有类型约束,可以 Set 任何内容。
修正示例:
func (s *Store) GetContract(id string) (Contract, error) {// ...
}
func (s *Store) SetContract(id string, contract Contract) error {// ...
}
func (s *Store) GetCustomer(id string) (Customer, error) {// ...
}
func (s *Store) SetCustomer(id string, customer Customer) error {// ...
}
定义了太多方法这不是问题,结合上文的消费侧的 interface 用法,可以通过接口进行约束,比如只关心合约的存储:
type ContractStorer interface {GetContract(id string) (Contract, error)SetContract(id string, contract Contract) error
}
🌟 何时使用 any(在确实可以接受或返回任何类型参数的时候)
示例1:
func Marshal(v any) ([]byte, error) {// ...
}
标准库 encoding/json 中的 Marshal 函数用于序列化,自然可以接受所有类型参数。
示例2:
func (c *Conn) QueryContext(ctx context.Context, query string, args ...any) (*Rows, error) {// ...
}
针对查询语句的参数设置,如 SELECT * FROM FOO WHERE ID = ? AND NAME = ?。
2.9 何时使用范型(#9)
场景:针对一个输入的 map 编写一个 getKeys 函数,获取所有的 keys,map 的 key 和 value 可能有多种类型。
不使用范型:
func getKeys(m any) ([]any, error) {switch t := m.(type) {default:return nil, fmt.Errorf("unknown type: %T", t)case map[string]int:var keys []anyfor k := range t {keys = append(keys, k)}return keys, nilcase map[int]string:// ...}
}
缺陷:
- 用户调用 getKeys 方法后,还需要额外的断言去判读得到的切片是什么类型。
- 随着类型扩张代码无限扩张。
🌟 在函数中使用范型:
func getKeys[K comparable, V any](m map[K]V) []K {var keys []Kfor k := range m {keys = append(keys, k)}return keys
}
func main() {// 外部调用m := map[string]int{"one": 1,"two": 2,"three": 3,}keys := getKeys(m)fmt.Println(keys)
}
map 的 key 并不是所有数据类型都可以的,要求可以使用 == 进行比较,因此可以使用内置的 comparable 关键字描述一个可比较的类型。
// Go 内置 comparable 接口
type comparable interface{ comparable }
// Go 内置 any 类型(空接口)
type any = interface{}
Go 支持自定义范型类型:
type customConstraint interface {~int | ~string
}
func getKeys[K customConstraint, V any](m map[K]V) []K {var keys []Kfor k := range m {keys = append(keys, k)}return keys
}
~int 表示任何类型的底层是 int 的类型,而 int 只能表示准确的 int 类型。
举个例子:
type customConstraint interface {~intString() string
}
type customInt int
func (c customInt) String() string {return strconv.Itoa(int(c))
}
func Print[T customConstraint](t T) {fmt.Println(t.String())
}
func main() {Print(customInt(1))
}
因为 customInt 的底层是 int 类型,并且实现了 String 方法,因此可以传递给 customConstraint 接口定义的类型。
但如果将 customConstraint 接口中的 ~int 修改为 int,则出现编译错误:Type does not implement constraint 'customConstraint' because type is not included in type set ('int'),换言之这里必须传递 int 类型,但是由于又限制了需要实现 String 方法,int 作为基本类型,是没有实现 String 方法的,此时陷入进退两难。
🌟 在 struct 中使用范型:
type Node[T any] struct {Val Tnext *Node[T]
}
func (n *Node[T]) Add(next *Node[T]) {n.next = next
}
func main() {n1 := Node[int]{Val: 1}n2 := Node[int]{Val: 2}n1.Add(&n2)
}
⚠️ 不可以使用范型的场景:
type Foo struct {}
func (f Foo) bar[T any](t T) {}
// 报错:method cannot have type parameters
Go 当中,函数和方法的区别在于,是否有接受者,意思是声明了函数的归属,上述代码方法的接受者是一个普通的 struct,不允许使用类型参数(范型)。
如果要在方法中使用范型,则要求方法的接受者具有类型参数(范型)。
type Foo[T any] struct{}
func (f Foo[T]) bar(t T) {}
🌟 最佳实践:
不要过早使用范型设计,就像不要过早使用 interface,去发现它,而不是创造它。
2.10 没有意识到类型嵌入可能带来的问题(#10)
类型嵌套:结构 A 拥有一个未命名的结构 B 作为字段。
type Foo struct {Bar
}
type Bar struct {Baz int
}
foo := Foo{}
foo.Baz = 42
foo.Bar.Baz = 42 // 与前一步等价
通过结构嵌套,定义在 Bar 内的属性或者方法会被提升至 Foo,可以直接调用。
接口嵌套:通过嵌套组合接口
type ReadWriter interface {ReaderWriter }
🌟 类型嵌套的错误示例:
type InMem struct {sync.Mutexm map[string]int
}
func New() *InMem {return &InMem{m: make(map[string]int)}
}
func (i *InMem) Get(key string) (int, error) {i.Lock()v, contains := i.m[key]i.Unlock()return v, contains
}
模拟一个基于内存的并发安全的 map 存储,使用类型嵌套,将互斥锁操作提升至 InMem 层直接调用,看似方便,但使得锁操作直接对外暴露:
m := inmem.New()
m.Lock() // ??不应该对外暴露锁操作,应该封装在 Get 操作内
🌟 修正示例:
type InMem struct {mu sync.Mutex m map[string]int
}
func (i *InMem) Get(key string) (int, error) {i.mu.Lock()v, contains := i.m[key]i.mu.Unlock()return v, contains
}
🌟 使用嵌套的一个优秀案例:
type Logger struct {// 不使用嵌套writeCloser io.WriteCloser
}
func (l Logger) Write(p []byte) (int, error) {return l.writeCloser.Write(p)
}
func (l Logger) Close() error {return l.writeCloser.Close()
}
-------------------------------------------------
type Logger struct {// 使用嵌套io.WriteCloser
}
func main() {l := Logger{WriteCloser: os.Stdout}_, _ = l.Write([]byte("foo"))_ = l.Close()
}
io.WriteCloser 是一个接口,声明了 Write 和 Close 两个方法,在不使用嵌套的代码中,必须为 Logger 类重新声明 Write 和 Close 方法,就为了对应去转发调用 io.WriteCloser 的两个方法,十分冗余。
使用嵌套接口之后,io.WriteCloser 类型的两个方法提升至 Logger 结构层,可以直接调用。这样也意味着 Logger 此时可以被视为实现了 io.WriteCloser 接口。
⚠️ 注意:当 Logger 嵌套了
io.WriteCloser,但初始化的时候不传入具体实现类os.Stdout,在编译 l.Write([]byte(“foo”)) 的时候会报错。
🌟 嵌套与面向对象编程的子类化的区别
下面是 Y 结构获得 X 的 Foo 方法的两种实现:
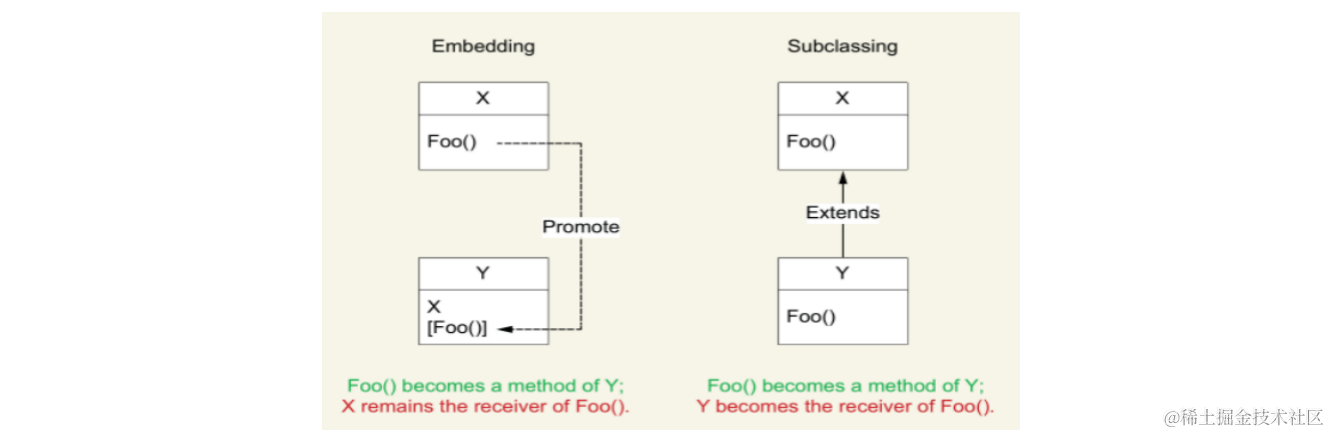
- 嵌套(左):X 保留对方法 Foo 的持有
- 子类化(右):Y 获得方法 Foo 的持有
🌟 总结:嵌套是一种组合的概念,而子类化是一种继承的概念。
Go 示例:
package main
import "fmt"
type X struct{}
func (x X) method() {fmt.Println("X's method")
}
type Y struct {X
}
func main() {y := Y{}y.method() // 调用 Y 中嵌套的 X 类型的 method,X 仍然是接收者
}
在上述示例中,Y 结构体嵌套了 X 结构体,当调用 Y 类型的实例的 method 方法时,接收者仍然是 X 类型,因此输出为 “X’s method”。
Java 示例:
class X {void method() {System.out.println("X's method");}
}
class Y extends X {// Y 没有显式声明 method,但继承了 X 的 method
}
public class Main {public static void main(String[] args) {Y y = new Y();y.method(); // 调用 Y 中继承的 X 类型的 method,Y 成为接收者}
}
在 Java 中,继承是一种机制,子类(派生类)继承了父类(基类)的方法,但对于方法调用,接收者(receiver)是实际的对象类型。因此,当在 Java 中使用继承时,调用子类的方法会使得子类成为接收者。
🌟 使用嵌套的两个原则:
- 不应该只为了访问变量的方便(语法糖)使用嵌套(例如上文使用
Foo.Baz替代Foo.Bar.Baz)。 - 不应该将需要内聚的方法或者字段提升到外层(例如上文的 mutex)。
⚠️ 注意:如果要嵌套一个频繁迭代的结构,外部结构需要考量这个内嵌结构的变动对外部结构的长远影响。或许不内嵌一个公共的 struct 是一个好的选择。
小结
您已完成学习进度10/100,再接再厉。