农药化肥网站建设商城网站建设教学
Django初次体验
关于django的安装,宝宝们可以参考django简介以及安装
Django框架的搭建
在终端中进入需要建立项目的目录
执行:
django-admin startproject mysite
其中,mysite是项目目录名,可以自定义
我们来看看startproject创建的内容:

关于上面自动生成的目录与文件解释如下:
- 外部的目录只是一个项目的容器。它的名字与Django无关; 您可以将其重命名为您喜欢的任何内容。
- manage.py:一个命令行实用程序,可以让您以各种方式与此Django项目进行交互。你可以阅读所有的细节 manage.py在Django的管理和manage.py。
- 内部mysite/目录是您的项目的实际Python包。它的名字是您需要用来导入其中的任何内容的Python包名称(例如mysite.urls)。
- mysite/init.py:一个空的文件,告诉Python这个目录应该被认为是一个Python包。
- mysite/settings.py:此Django项目的设置/配置。 Django设置会告诉你所有关于设置的工作原理。
- mysite/urls.py:该Django项目的URL声明; 您的Django动力网站的“目录”。
- mysite/wsgi.py:WSGI兼容的Web服务器为您的项目提供服务的入口点。
启动项目
在终端中进入当前 manage.py的文件目录下 执行一下命令
python manage.py runserver
您将在命令行中看到以下输出:
Watching for file changes with StatReloader
Performing system checks...System check identified no issues (0 silenced).You have 17 unapplied migration(s). Your project may not work properly until you apply the migrations for app(s): admin, auth, con
tenttypes, sessions.
Run 'python manage.py migrate' to apply them.
July 22, 2019 - 19:29:14
Django version 2.2.3, using settings 'mysite.settings'
Starting development server at http://127.0.0.1:8000/
Quit the server with CTRL-BREAK.
浏览器访问
然后我们可以去浏览器中访问http://127.0.0.1:8000/
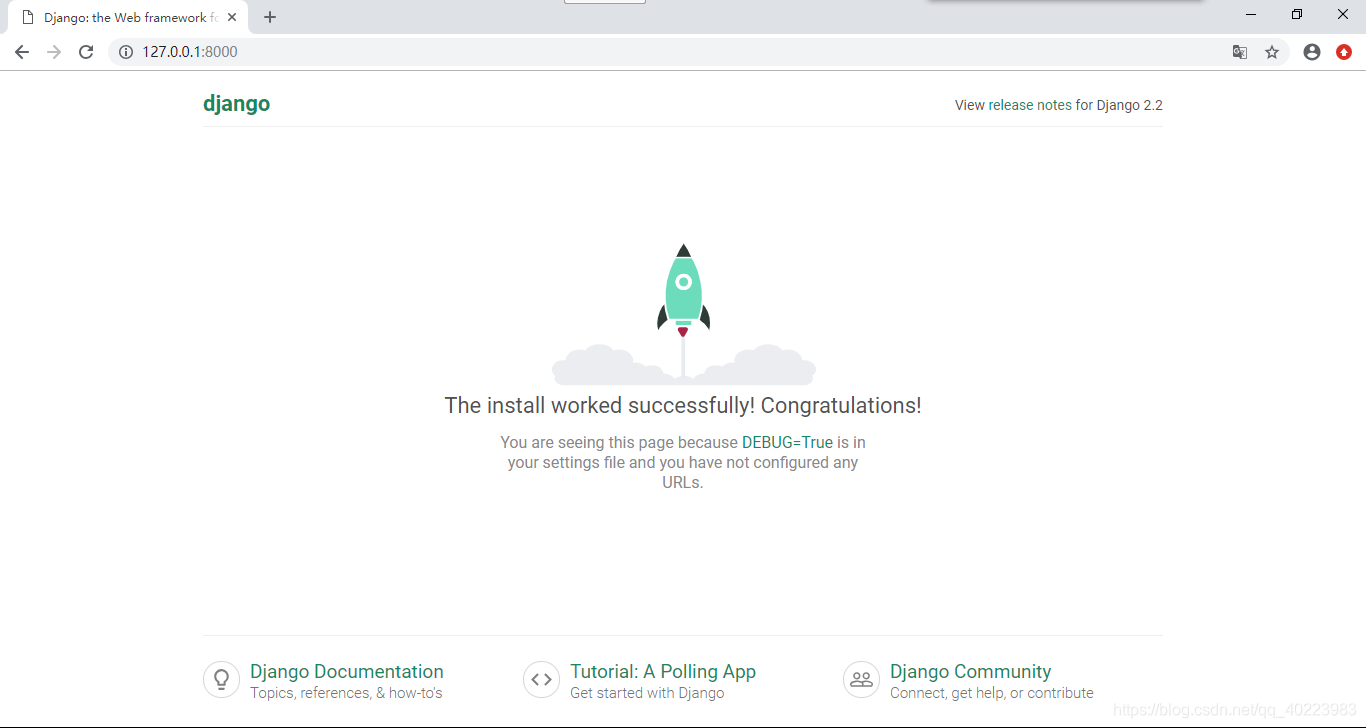
这个页面表示django创建成功,并且正在本机运行。
后续内容更加精彩,请持续关注小编的博客
