在Qt中设置widget背景颜色或者图片方法很多种:重写paintEvent() , 调色板QPalette , 样式表setStyleSheet等等。
但是各种方法都有其注意事项,如果不注意则很容易陷入麻烦中。
1:setStyleSheet()
这个函数我一直很喜欢使用,因为只要写一句就可以实现效果,比其他方法都简单,但是其却有一个很值得注意的地方,也就是这个地方让我大吃苦头。
亦即:①:该函数只能用于设置有父窗口的子窗口的背景!如果一个窗口没有子窗口,则无法使用该函数来设置背景颜色或图 片!!
②:同时:对于一个父窗口而言:如果我们用setStyleShette设置了其样式,而对于其子窗口:如果没有用同样的函数来设 置的话, 则其子窗口的样式和其父窗口完全一致,亦即:其集成了自己父窗口的样式!
③:延伸:对顶层窗口(没有父窗口),其有若干个子窗口,则当我们用setStyleShette来设置这个顶层窗口的样式后,依据①可知:该父窗口本身没有任何变化,亦即设置没有生效;而其子窗口:只要子窗口本身没有用setStyleShette来设置自己的样式表,则其就是用的自己父窗口的样式表!!
例如:
主窗口(没有父类)为MainWin
MainWin::MainWin()
{
this->setStyleSheet("background-image:url(:/bmp/IMG_0345.JPG)");
iButton = new QPushButton(this);
iLabel = new QLabel(iButton);
}
运行一下,效果如下:
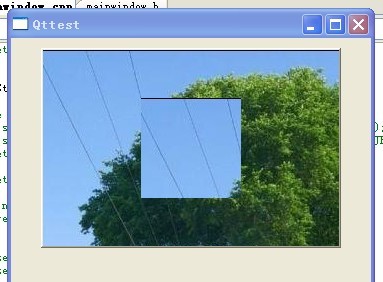
亦即:虽然我们设置的是顶层的父窗口,但是该样式却是在其子窗口中生效,而顶层父窗口没有任何变化! 这验证了①。
修改一下上例代码:
MainWin::MainWin()
{
this->setStyleSheet("background-image:url(:/bmp/IMG_0345.JPG)");
iButton = new QPushButton(this);
iLabel = new QLabel(iButton);
iLabel->setStyleSheet("background-image:url(:/bmp/1257253475842.jpg)");
}
则运行效果如下:
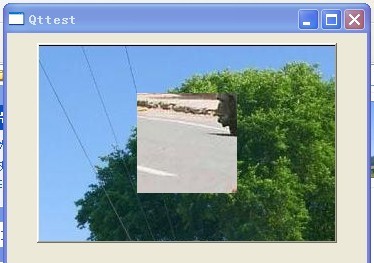
可见:子窗口只有调用setStyleSheet()设置了自己的样式后才可以隔断父窗口的样式,否则其将是用父窗口的样式。
再修改一下代码:
MainWin::MainWin()
{
iButton = new QPushButton(this);
iButton ->setStyleSheet("background-image:url(:/bmp/IMG_0345.JPG)");
iLabel = new QLabel(iButton);
}
运行一下,效果如下:
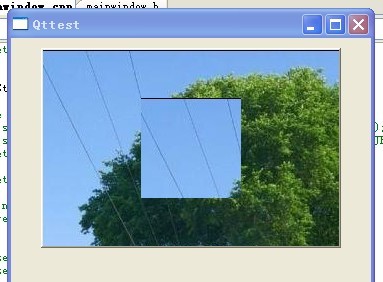
可见:设置有父窗口的子窗口时:setStyleSheet()一定生效!!!
后来我又思考了一个问题,那就是:对于顶层父窗口,如果我setStyleSheet()设置了样式表,而对其子窗口,我用其他方法,比如用QPalette调色板来设置背景图片/颜色,这时子窗口的背景到底是由继承自父窗口的样式表决定呢还是由子窗口本身的QPalette调色板决定呢?
再次修改代码:
MainWin::MainWin()
{
this->setStyleSheet("background-image:url(:/bmp/IMG_0345.JPG)");
iButton = new QPushButton(this);
iLabel = new QLabel(iButton);
QPalette palette;
palette.setBrush(iLabel->backgroundRole(),QBrush(QImage(":/bmp/1257253475842.jpg")));
iLabel->setPalette(palette);
iLabel->setAutoFillBackground(true);
}
此段代码中我用QPalette来设置子窗口的背景图片,看下到底是样式表还是调色板生效,效果如下
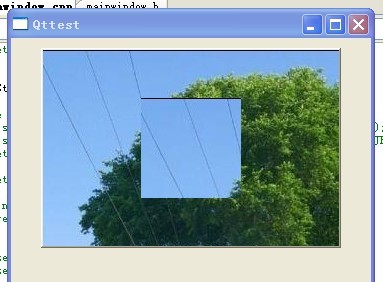
由此可见:一旦顶层窗口设置了样式表,则其子窗口无论用什么方法来设置背景,都会不生效!!!
那如果不是顶层窗口而仅仅是一般窗口设置了样式表呢?再次修改代码:
MainWin::MainWin()
{
iButton = new QPushButton(this);
iButton ->setStyleSheet("background-image:url(:/bmp/IMG_0345.JPG)");
iLabel = new QLabel(iButton);
QPalette palette;
palette.setBrush(iLabel->backgroundRole(),QBrush(QImage(":/bmp/1257253475842.jpg")));
iLabel->setPalette(palette);
iLabel->setAutoFillBackground(true);
}
运行效果同上,这说明:不管是顶层窗口还是一般窗口,只要用setStyleSheet设置了样式表,则其子窗口用其它方式设置背景颜色/图片均不生效,只能用同样方式setStyleSheet来设置更改!!!
为了验证上边的结论,再次修改代码:
MainWin::MainWin()
iButton = new QPushButton(this);
iLabel = new QLabel(iButton);
QPalette palette;
palette.setBrush(iLabel->backgroundRole(),QBrush(QImage(":/bmp/1257253475842.jpg")));
iLabel->setPalette(palette);
iLabel->setAutoFillBackground(true);
}
运行一下:
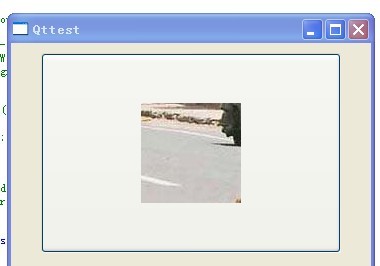
此时调色板才生效,这也间接证明了上述结论。
==========================================================================
总结:
1:不要在顶层窗口(无父类的窗口)中使用setStyleSheet() ,否则其一父窗口的背景不会改变,其次其子窗口的背景设置方法变得局限唯一,不能再使用其它方法!
2:如果一个一般窗口(非顶层窗口)还有子窗口,那最好不要使用setStyleSheet()来设置其背景颜色,因为虽然此时该窗口的背景设置是生效的,但是其子窗口的背景设置也变得局限唯一,只能使用setStyleSheet,而不能使用其它方法! 当然:你如果就是只想使用这种方法,那也完全可以!!
说白了就是:不要再MainWindow中使用setStyleSheet()!
而上边之所以强调拓宽子窗口设置背景的方法范围,这是因为:如果只能用setStyleSheet样式表来设置背景图片的话,该图片是无法缩放的,如果其大小与widget窗口大小不相符,则我们无法用程序来实现图片的缩放,除非我们直接处理图片使其大小与widget窗口相符; 而如果不局限于用setStyleSheet样式表来设置的话,我们可以选择用QPalette调色版,其内部setBrush()之前,我们完全可以先对图片进行scale缩放再刷到窗口上,这样就避免直接去处理图片,灵活性强一点!
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/NRC_DouNingBo/archive/2010/05/07/5565212.aspx
