网站维修合同网站已备案 还不能访问
在介绍 Clone 最终篇之前,我们先简要回顾一下前面所讲的内容。在第一篇中,我们探讨了 Clone 的用途、使用的前提条件、存在的限制,以及它的备份原理。Clone 是一种用于复制和备份数据的工具,它能够快速高效地创建数据的精确副本。使用 Clone 需要满足一定的前提条件,同时还需要注意一些限制。
在第二篇中,我们深入探讨了如何通过 Clone 进行本地克隆数据。 本地克隆操作从MySQL服务器实例中克隆数据,其中克隆操作启动到MySQL服务器实例运行的同一服务器或节点上的目录。通过 Clone 进行本地克隆数据需要遵循一定的步骤,包括选择要克隆的源和目标位置、配置 Clone 参数、执行克隆操作等。完成克隆后,我们可以验证数据的完整性和一致性。
今天,在第三篇中,我们将介绍如何通过 Clone 进行远程克隆数据。远程克隆是指将数据从源位置复制到远程服务器或云存储位置的过程。与本地克隆相比,远程克隆需要更多的配置和设置,以确保数据能够安全地传输到远程位置。我们将详细介绍如何配置远程克隆的参数、执行远程克隆操作以及验证数据的完整性和一致性。
别忘了点赞哦!否则我会觉得我的文章写得像是一堆废纸。

官方文档对远程克隆数据的详细介绍:
MySQL :: MySQL 8.0 Reference Manual :: 5.6.7.3 Cloning Remote Data
远程克隆数据的用途:
1、MGR节点快速扩充
2、主从复制的slave节点快速搭建(其实和MGR节点快速扩充操作时一样的,今天的案例以这种为主)
远程克隆数据语法:
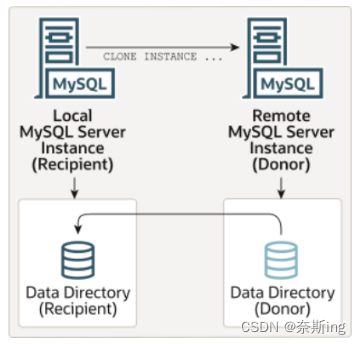
远程克隆操作涉及本地MySQL服务器实例(“recipient”)启动克隆操作的服务器,以及远程MySQL服务器实例(“donor”)源数据所在的位置。当对接收方启动远程克隆操作时,克隆的数据将通过网络从donor传输到recipient。默认情况下,远程克隆操作将删除recipient数据目录中的数据,并将其替换为已克隆的数据。还可以选择将数据复制到recipient上的其他目录,以避免删除现有数据。
语法:
CLONE INSTANCE FROM 'user'@'host':port
IDENTIFIED BY 'password'
[DATA DIRECTORY [=] 'clone_dir']
[REQUIRE [NO] SSL]; ---用户需要有BACKUP_ADMIN权限
DATA DIRECTORY:是一个可选子句,用于在接收端指定要克隆的数据的目录。如果不想删除recipient原数据目录中的现有数据,可以使用此选项修改数据copy的目录,必须有绝对路径,且目录必须不存在。不指定的话,则默认克隆到Recipient的数据目录下。
[REQUIRE [NO] SSL]:显式指定在通过网络传输克隆数据时是否使用加密连接。如果不能满足显式规范,则返回错误。如果未指定SSL子句,克隆将在默认情况下尝试建立加密连接,如果安全连接尝试失败,则返回到不安全连接。无论是否指定此子句,克隆加密数据时都需要安全连接。
如何停止远程克隆:
SQL> select * from performance_schema.clone_status\G; ---克隆操作的状态
PID:Processlist ID。对应show processlist中的Id,如果要终止当前的克隆操作,执行kill processlist_id命令即可。
SQL> Kill+id号;
远程克隆相关视图:
SQL> select * from performance_schema.clone_status\G; ---克隆操作的状态
PID:Processlist ID。对应show processlist中的Id,如果要终止当前的克隆操作,执行kill processlist_id命令即可。
STATE:克隆操作的状态,Not Started(克隆尚未开始),In Progress(克隆中),Completed(克隆成功),Failed(克隆失败)。如果是Failed状态,ERROR_NO,ERROR_MESSAGE会给出具体的错误编码和错误信息。
BEGIN_TIME:克隆操作开始
END_TIME:克隆结束时间。
SOURCE:Donor(源库)实例的地址。
DESTINATION:克隆目录。“LOCAL INSTANCE”代表当前实例的数据目录。
BINLOG_FILE:克隆完成后的file号
BINLOG_POSITION:file的pos点
GTID_EXECUTED:克隆的gtid点,可利用这些信息来搭建从库。
SQL> select
stage,
state,
cast(begin_time as DATETIME) as "START TIME",
cast(end_time as DATETIME) as "FINISH TIME",
lpad(sys.format_time(power(10,12) * (unix_timestamp(end_time) - unix_timestamp(begin_time))), 10, ' ') as DURATION,
lpad(concat(format(round(estimate/1024/1024,0), 0), "MB"), 16, ' ') as "Estimate",
case when begin_time is NULL then LPAD('%0', 7, ' ')
when estimate > 0 then
lpad(concat(round(data*100/estimate, 0), "%"), 7, ' ')
when end_time is NULL then lpad('0%', 7, ' ')
else lpad('100%', 7, ' ')
end as "Done(%)"
from performance_schema.clone_progress;
STAGE:一个克隆操作可依次细分为DROP DATA,FILE COPY,PAGE COPY,REDO COPY,FILE SYNC,RESTART,RECOVERY等7个阶段。当前阶段结束了才会开始下一个阶段。本地克隆只涉及到前五个阶段完成DROP DATA,FILE COPY,PAGE COPY,REDO COPY,FILE SYNC,远程克隆涉及到七个阶段
STATE:当前阶段的状态。有三种状态:Not Started,In Progress,Completed。
BEGIN_TIME:当前阶段的开始时间和结束时间。
END_TIME:当前阶段的开始时间和结束时间。
THREADS:当前阶段使用的并发线程数。并发线程数一般由clone_autotune_concurrency参数自动调节。默认为ON,此时该参数最大线程数受clone_max_concurrency参数控制。若设置为OFF,则并发线程数的数量将是固定的同clone_max_concurrency参数保持一致。clone_max_concurrency参数的默认值为16。
ESTIMATE:预估的数据量。
DATA:已经拷贝的数据量。
NETWORK:通过网络传输的数据量。如果是本地克隆,该列的值为0。
DATA_SPEED:当前数据拷贝的速率。注意,是当前值。
NETWORK_SPEED:当前网络传输的速率。注意,是当前值。
案例开始(通过远程克隆对主从复制的slave节点快速搭建):

1、主库(Donor)上的配置
(1)将1个从库的域名加入到hosts文件
[root@mysql1 ~]# vi /etc/hosts
192.168.56.31 mysql1 ---原有域名解析 192.168.56.32 mysql2(2)创建二进制和中继日志目录(如果主库已经开了二进制日志则不需要配置)
[root@mysql1 ~]# mkdir -p /mysql/log/3306/binlog ---二进制目录日志
[root@mysql1 ~]# mkdir -p /mysql/log/3306/relaylog ---中继日志目录
[root@mysql1 ~]# chown -R mysql:mysql /mysql/log/3306/binlog
[root@mysql1 ~]# chown -R mysql:mysql /mysql/log/3306/relaylog
[root@mysql1 ~]# chmod -R 775 /mysql/log/3306/binlog
[root@mysql1 ~]# chmod -R 775 /mysql/log/3306/relaylog
(3)配置相关参数
[root@mysql1 ~]# cp /etc/my.cnf /etc/my.cnf.bak
[root@mysql1 ~]#vi /etc/my.cnf
###binlog### binlog_gtid_simple_recovery=1 ---(默认值)这个参数控制了当mysql启动或重启时,mysql在搜寻GTIDs时是如何迭代使用binlog文件的。这个选项设置为真,会提升mysql执行恢复的性能。因为这样mysql-server启动和binlog日志清理更快 log_bin=/mysql/log/3306/binlog/itpuxdb-binlog ---二进制输出路径(指定之后将指定的值赋给log_bin_basename这个参数上,log_bin显示为on,bug) log_bin_index=/mysql/log/3306/binlog/itpuxdb-binlog.index ---记录二进制日志文件的基本名称和路径在这个可读的文件中。默认和log_bin参数的值相同,并在此基础上会自动加上扩展名.index binlog_format=ROW ----二进制工作模式,’ROW’会记录每一行数据被修改的情况(必须) binlog_rows_query_log_events=on ----二进制日志中记录更详细的SQL操作。一个事务就是一个事件,binary log events expire_logs_days = 10 ----二进制日志保留天数(根据业务安排,官方表示只删除二进制。中继日志由relay_log_purge参数控制在sql线程应用完之后自动清理,默认为on启用)(4)Clone(数据克隆)插件安装
mysql> INSTALL PLUGIN clone SONAME 'mysql_clone.so'; ---这种是手动在线安装插件,不需要重启,并且重启后也不会失效。
mysql> show plugins;
(5)主从库创建复制用户并授权
mysql> create user 'repuser'@'%' identified with mysql_native_password BY '123456';
mysql> grant replication client,replication slave on *.* to 'repuser'@'%';
mysql> flush privileges;
mysql> select user,host from mysql.user;
(5)在Donor实例上创建克隆用户(用于recipient端复制)
mysql> create user 'donor_clone_user'@'%' identified by '123456';
mysql> grant backup_admin on *.* to 'donor_clone_user'@'%';
2、从库(recipient)上的配置
(1)将主从库的域名加入到hosts文件
[root@mysql2 ~]# vi /etc/hosts
192.168.56.31 mysql1 192.168.56.32 mysql2(2)创建二进制和中继日志目录
[root@mysql2 ~]# mkdir -p /mysql/log/3306/binlog ---二进制目录日志
[root@mysql2 ~]#mkdir -p /mysql/log/3306/relaylog ---中继日志目录
[root@mysql2 ~]#chown -R mysql:mysql /mysql/log/3306/binlog
[root@mysql2 ~]#chown -R mysql:mysql /mysql/log/3306/relaylog
[root@mysql2 ~]#chmod -R 775 /mysql/log/3306/binlog
[root@mysql2 ~]#chmod -R 775 /mysql/log/3306/relaylog
(3)配置相关参数
[root@mysql2 ~]#cp /etc/my.cnf /etc/my.cnf.bak
[root@mysql2 ~]#vi /etc/my.cnf
###binlog### binlog_gtid_simple_recovery=1 ---(默认值)这个参数控制了当mysql启动或重启时,mysql在搜寻GTIDs时是如何迭代使用binlog文件的。这个选项设置为真,会提升mysql执行恢复的性能。因为这样mysql-server启动和binlog日志清理更快 log_bin=/mysql/log/3306/binlog/itpuxdb-binlog ---二进制输出路径(指定之后将指定的值赋给log_bin_basename这个参数上,log_bin显示为on,bug) log_bin_index=/mysql/log/3306/binlog/itpuxdb-binlog.index ---记录二进制日志文件的基本名称和路径在这个可读的文件中。默认和log_bin参数的值相同,并在此基础上会自动加上扩展名.index binlog_format=ROW ----二进制工作模式,’ROW’会记录每一行数据被修改的情况(必须) binlog_rows_query_log_events=on ----二进制日志中记录更详细的SQL操作。一个事务就是一个事件,binary log events expire_logs_days = 10 ----二进制日志保留天数(根据业务安排,官方表示只删除二进制。中继日志由relay_log_purge参数控制在sql线程应用完之后自动清理,默认为on启用)###slave parameter### max_relay_log_size ---中继日志大小,默认为0,可以手动定义大小。官方表示如果max_relay_log_size为0,那么将继承max_binlog_size二进制日志大小(继承二进制大小即可,默认1G大小) relay_log=/mysql/log/3306/relaylog/itpuxdb_relay ---中继日志输出路径 relay_log_index=/mysql/log/3306/relaylog/itpuxdb_relay.index ---中继日志索引输出路径(根据生产而定) slave_parallel_type=LOGICAL_CLOCK ---默认DATABASE值,兼容MySQL 5.6基于schema级别的并发复制,基于库的并行复制方式; LOGICAL_CLOCK值:基于组提交的并行复制方式,组提交是一堆事务的集合,减轻1O压力(之前是采用一个事务提交一次,设置为LOGICAL_CLOCK后多个事务执行完成后提交一次,减轻IO压力)。 super_read_only=1 ---Slave机器上对数据库进行修改或者删除,会导致主从的不一致,需要对Slave机器设置为read_only=1让Slave提供只读操作。read_only仅仅对没有SUPER权限的用户有效(即mysql.user表的Super_priv字段为Y),一般给App的权限是不需要SUPER权限的。参数super_read_only可以将有SUPER权限的用户也设置为只读,且该参数设置为ON后 read_only也跟着自动设置为ON slave_parallel_workers=4 ---4个sql_thread(coordinator线程)来进行并行复制,可以动态调整复制线程数(是四个SQL线程,IO线程还是一个)。并且需要重启主从复制生效 relay_log_recovery=1 ---IO线程安全。支持中继日志自我修复功能,日志丢失损坏时,从主master获取日志,完成日志的恢恢复(该参数表示当前接受到的relay log全部删除,然后从sql线程回放到的位置重新拉取) relay_log_info_repository=table ---SQL线程安全。默认是file,SQL线程的数据回放是写数据库操作,relay-info是写文件操作。这两个操作很难保证一致性,relay-info将写入到mysql.slave_relay_log_info这张表中 master_info_repository=table ---默认是file,IO线程也是接收一个个的event。通过设置参数master_info_repository可以将master-info信息写到什么位置,性能上比设置为FILE有很高的提升,可靠性也得到保证,设置为TABLE后,master-info将信息保存到mysql.slave_master_info slave_skip_errors=ddl_exist_errors ---解决ddl语句在从库造成冲突,可设置off,all,ErorCode,ddl_exist_erros选项。默认为off。如果使用show slave status\G中看到last_Errno:1062,那么设置slave_skip_errors=1062,slave_skip_errors=all,slave_skip_errors=ddl_exist_errors解决 slave_preserve_commit_order=1 ---slave上commit的顺序保持一致,必须为1,否则可能会有GAP锁产生(4)Clone(数据克隆)插件安装
mysql> INSTALL PLUGIN clone SONAME 'mysql_clone.so'; ---这种是手动在线安装插件,不需要重启,并且重启后也不会失效。
mysql> show plugins;
(5)主从库创建复制用户并授权
mysql> create user 'repuser'@'%' identified with mysql_native_password BY '123456';
mysql> grant replication client,replication slave on *.* to 'repuser'@'%';
mysql> flush privileges;
mysql> select user,host from mysql.user;
(6)在Recipient实例上创建克隆用户(用于recipient连接)
mysql> create user 'recipient_clone_user'@'%' identified by '123456';
mysql> grant clone_admin on *.* to 'recipient_clone_user'@'%';
(7)设置克隆期间允许DDL(为了在克隆期间允许DDL,设置clone_ddl_timeout参数为0,虽然会导致克隆失败但要保证DDL不受影响。8.0.27版本新增clone_block_ddl参数在克隆期间允许DDL同时不会导致克隆失败。这个设置可选)
mysql> set global clone_ddl_timeout=0; ---设置为0意味着克隆操作不会等待备份锁。在这种情况下,执行并发DDL操作可能导致克隆操作失败,设置为其他数值发现还是需要等到克隆完成,只有设置为0。
(8)在Recipient上设置Donor白名单,只克隆白名单中的实例
mysql> set global clone_valid_donor_list = '192.168.56.31:3306'; ----Donor主库的ip和端口
(9)在Recipient上发起克隆命令
[root@slave ~]# mysql -urecipient_clone_user -p123456 -S /mysql/data/3306/mysql.sock
mysql> clone instance from 'donor_clone_user'@'192.168.56.31':3306 identified by '123456'; ---从库完成DROP DATA,FILE COPY,PAGE COPY,REDO COPY,FILE SYNC后,在RESTART阶段进行重启实例,在启动的过程中会用xxx.#clone替换掉原来的系统表空间文件,最后进行RECOVERY
(10)查看克隆操作
mysql> select * from performance_schema.clone_status\G; ---克隆操作的状态
PID:Processlist ID。对应show processlist中的Id,如果要终止当前的克隆操作,执行kill processlist_id命令即可。
STATE:克隆操作的状态,Not Started(克隆尚未开始),In Progress(克隆中),Completed(克隆成功),Failed(克隆失败)。如果是Failed状态,ERROR_NO,ERROR_MESSAGE会给出具体的错误编码和错误信息。
BEGIN_TIME:克隆操作开始
END_TIME:克隆结束时间。
SOURCE:Donor(源库)实例的地址。
DESTINATION:克隆目录。“LOCAL INSTANCE”代表当前实例的数据目录。
BINLOG_FILE:克隆完成后的file号
BINLOG_POSITION:file的pos点
GTID_EXECUTED:克隆的gtid点,可利用这些信息来搭建从库。
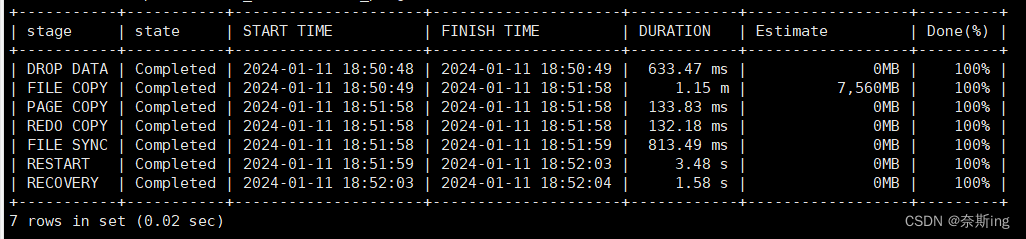
mysql> select stage,state,cast(begin_time as DATETIME) as "START TIME",cast(end_time as DATETIME) as "FINISH TIME",lpad(sys.format_time(power(10,12) * (unix_timestamp(end_time) - unix_timestamp(begin_time))), 10, ' ') as DURATION,lpad(concat(format(round(estimate/1024/1024,0), 0), "MB"), 16, ' ') as "Estimate",case when begin_time is NULL then LPAD('%0', 7, ' ')when estimate > 0 thenlpad(concat(round(data*100/estimate, 0), "%"), 7, ' ')when end_time is NULL then lpad('0%', 7, ' ')else lpad('100%', 7, ' ')end as "Done(%)"from performance_schema.clone_progress;STAGE:一个克隆操作可依次细分为DROP DATA,FILE COPY,PAGE COPY,REDO COPY,FILE SYNC,RESTART,RECOVERY等7个阶段。当前阶段结束了才会开始下一个阶段。本地克隆只涉及到前五个阶段完成DROP DATA,FILE COPY,PAGE COPY,REDO COPY,FILE SYNC,远程克隆涉及到七个阶段
STATE:当前阶段的状态。有三种状态:Not Started,In Progress,Completed。
BEGIN_TIME:当前阶段的开始时间和结束时间。
END_TIME:当前阶段的开始时间和结束时间。
THREADS:当前阶段使用的并发线程数。并发线程数一般由clone_autotune_concurrency参数自动调节。默认为ON,此时该参数最大线程数受clone_max_concurrency参数控制。若设置为OFF,则并发线程数的数量将是固定的同clone_max_concurrency参数保持一致。clone_max_concurrency参数的默认值为16。
ESTIMATE:预估的数据量。
DATA:已经拷贝的数据量。
NETWORK:通过网络传输的数据量。如果是本地克隆,该列的值为0。
DATA_SPEED:当前数据拷贝的速率。注意,是当前值。
NETWORK_SPEED:当前网络传输的速率。注意,是当前值。
(10)验证从库数据
[root@mysql1 data]# mysql
mysql> show databases;
mysql> select table_name from information_schema.tables;
mysql> select * from ded.itpuxbak11;
mysql> select * from itpuxdb.emp;
mysql> select * from itpuxdb.yg; ---能查询到数据,表示数据恢复的没问题。可能存在表不能查询的情况,那么就是数据字典没有记录表的问题,需要多验证几张
(11)在从库上使 slave 与 master 建立连接
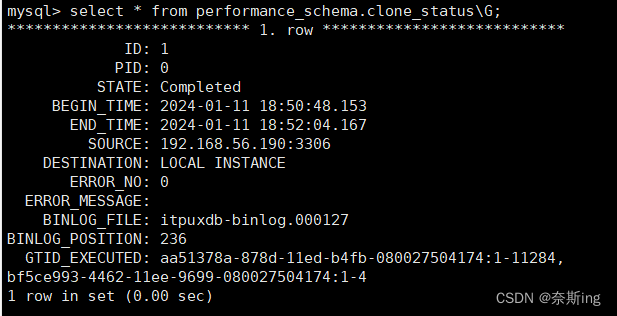
mysql> select * from performance_schema.clone_status\G;
通过clone在线数据克隆的相关视图得知,备份时当时的二进制写入的是binlog.000127日志,pos点为236。Gtid为aa51378a-878d-11ed-b4fb-080027504174:1-11284,bf5ce993-4462-11ee-9699-080027504174:1-4,那么通过gtid无损复制需要指定gtid,show master status;的值
mysql> set @MYSQLDUMP_TEMP_LOG_BIN = @@SESSION.SQL_LOG_BIN;
mysql> set @@SESSION.SQL_LOG_BIN= 0;
mysql> set @@GLOBAL.GTID_PURGED='db71491a-4105-11ec-b44d-08002745a35a:1-264'; ---指定gtid_purged为clone在线数据克隆备份时的gtid点,就是通知数据库这个gtid之前的事务被清除了(也是就记录自动清理或者手动清理的二进制最后的全局事务ID),向设置的gtid_purged点开始向后复制事务。如果有多个事务,用逗号分隔即可
mysql> set @@SESSION.SQL_LOG_BIN = @MYSQLDUMP_TEMP_LOG_BIN;
mysql> Show variables like '%gtid%';
mysql> change master to master_host='192.168.56.31', master_port=3306, master_user='repuser', master_password='123456', master_auto_position=1; ---GTID replication采用自动定位binlog+positionmysql> start slave; ----启动主从复制
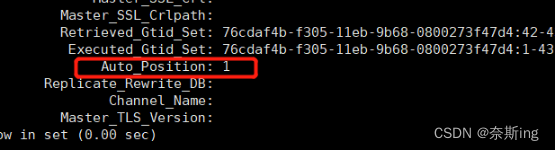
mysql> show slave status \G; ----Auto_Position为1:使用的就是GTID技术,GTID replication采用自动binlog+position。
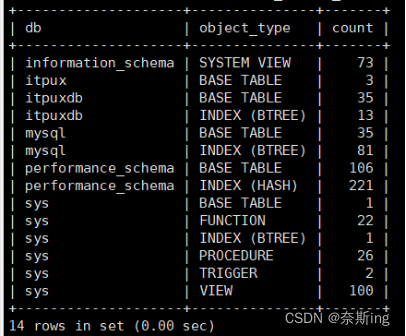
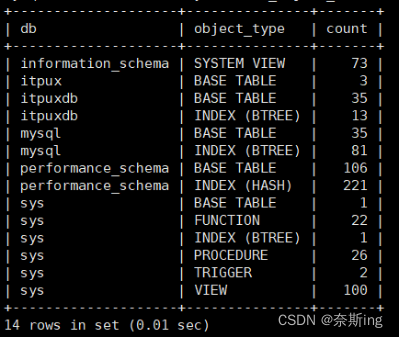
(12)验证对象数量
mysql> select * from sys.schema_object_overview where db='itpuxdb'; ---数据对象