赚钱的网站平台珠海网站建设优化
目录
1.数据结构--并查集
2.数据结构--图
1.图的基础概念
2.图的简单实现
2.1.邻接矩阵的图实现
2.2.邻接表的图实现
2.3.图的DFS和BFS
2.4.最小生成树
2.4.1.Kruskal(克鲁斯卡尔算法)
2.4.2.Prim(普里姆算法)
2.5.最短路径
2.5.1.Dijkstra(迪杰斯特拉算法)
2.5.2.Bellman-Ford(贝尔曼-福特算法)
2.5.3.Floyd-Warshall(弗洛伊德算法)
1.数据结构--并查集
概念:将n个不同的元素划分成一些不相交的集合。
- 开始时,每个元素自成一个单元素集合;初始化
- 然后按一定的规律将归于同一组元素的集合合并;合并
- 在此过程中要反复用到查询某一个元素归属于那个集合的运算:查询 适合于描述这类问题的抽象数据类型称为并查集(union-find set)
概念图:

实现:Count:遍历数组元素有多少个负数,就有几个集合
#pragma once
#include<iostream>
#include<vector>
#include<unordered_map>
using namespace std;template<class T>
class UnionFindSet {
public:int Find(T val){int index = _find_index[val];while (_v[index] >= 0)index = _v[index];return index;}bool Union(T x, T y){int xi = Find(x);int yi = Find(y);//是否已经联合了if (xi == yi)return false;_v[xi] += _v[yi];_v[yi] = xi;return true;}//有多少个集合int Count(){int count = 0;for (auto e : _v){if (e < 0)count++;}return count;}
public:UnionFindSet(const vector<T>& tmp){for (int i = 0; i < tmp.size(); i++)_find_index[tmp[i]] = i;_v.resize(tmp.size(), -1);}~UnionFindSet(){}
private://vector<T> _v;//哈希数组的数据和下标unordered_map<T, int> _find_index;
};测试:
#include<iostream>
#include"UnionFindSet.h"
#include<string>using namespace std;int main()
{vector<int> v{ 1,23,432,5345,8,712,44,534,645,73,862,3 };UnionFindSet<int> ufs(v);ufs.Union(1, 534);ufs.Union(1, 534);ufs.Union(73, 534);ufs.Union(1, 4);ufs.Union(23, 8);ufs.Union(862, 73);ufs.Union(3,3);cout << ufs.Count() << endl;return 0;
}可以试试这个题:使用并查集做
Leetcode:省份数量
class UnionFindSet{public:int Find(int x){//找到下标int index = _find_index[x];while(_v[index] >= 0){index = _v[index] ;}return index;}bool Union(int x, int y){int xi = Find(x);int yi = Find(y);//已经联合if(xi == yi)return false;_v[xi] += _v[yi];_v[yi] = xi;return true;}int Count(){int count = 0;for(auto e : _v){if(e < 0)count++;}return count;}public:UnionFindSet(const vector<int>& v){_v.resize(v.size(), -1);for(int i = 0; i<v.size();i++)_find_index[i] = i;}private:vector<int> _v;unordered_map<int, int> _find_index;
};class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {int n = isConnected.size();vector<int> v;for(int i =0; i<n; i++){v.push_back(i);}UnionFindSet ufs(v);for(int i = 0; i<n; i++){for(int j=0; j<n; j++){if(isConnected[i][j] == 1){ufs.Union(i,j);}}}return ufs.Count();}
};2.数据结构--图
1.图的基础概念
图(graph):由顶点(vertex)集合和顶点之间的关系(edge)构成,即G = (V, E);
- 顶点:图内的任意顶点;
- 边:连接两个顶点;
- 边的权值:连接两个顶点的边的值;
无向图和有向图
- 无向图:两个顶点之间的边无方向,两个边的权值用一个数值表示 ; 所以为强关系图:例如:qq和微信的互相为好友关系
- 有向图:两个顶点之间的边有方向,代表的是一个顶点到另一个顶点的权值 ; 所以为弱关系图:例如 抖音关注主播,主播不会同时关注你

完全图:在有n个顶点的无向图中,若有n * (n-1)/2条边,即任意两个顶点之间有且仅有一条边, 则称此图为无向完全图,比如上图G1;在n个顶点的有向图中,若有n * (n-1)条边,即任意两个 顶点之间有且仅有方向相反的边,则称此图为有向完全图,比如上图G4。
顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v);。在有向图中,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度 是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。注意:对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。
简单路径与回路:若路径上各顶点v1,v2,v3,…,vm均不重复(不构成回路的路径),则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。
生成树:一个连通图的最小连通子图(整个图连通 ,任一顶点都可以找到另一顶点)称作该图的生成树。有n个顶点的连通图的生成树有n个顶点 和n-1条边。
2.图的简单实现
2.1.邻接矩阵的图实现
优势:使用邻接矩阵可以快速查找(时间复杂度O(1))两个顶点是否有边且边的权值;劣势:查找顶点的度时(时间复杂度为O(N));
设计理念:有n个顶点,创建一个n*n的二维矩阵来放置两个顶点边的权值,为空可以使用一个权值的最大值或者最小值;
#pragma once
#include<iostream>
#include<string>
#include<vector>
#include<unordered_map>
#include<unordered_set>
#include<queue>
#include"UnionFindSet.h"using namespace std;//V顶点类型,W权值类型
namespace Matrix {template<class V, class W, bool Direction = false, W W_MAX = INT_MAX>class Graph {public:typedef Graph<V, W, Direction, W_MAX> Self;int Find(const V& v){auto it = _find_index.find(v);if (it == _find_index.end())return -1;return it->second;}bool AddEdge(const V& src, const V& des, const W& weight){int si = Find(src);int di = Find(des);//错误顶点if (si == -1 || di == -1)return false;_matrix[si][di] = weight;if (Direction == false)_matrix[di][si] = weight;return true;}void Print(){for (int i = 0; i < _matrix.size(); i++){for (int j = 0; j < _matrix.size(); j++){if (_matrix[i][j] == W_MAX)printf("%5c", '*');elseprintf("%5d", _matrix[i][j]);}cout << endl;}}public:Graph(const vector<V>& v){int n = v.size();_vertexs.resize(n);//初始化顶点集合和 顶点和下标的映射for (int i = 0; i < n; i++){_vertexs[i] = v[i];_find_index[v[i]] = i;}//初始邻接矩阵_matrix.resize(n, vector<W>(n, W_MAX));}Graph() = default;~Graph(){}private://顶点集合vector<V> _vertexs;//查找顶点下标unordered_map<V, int> _find_index;vector<vector<W>> _matrix;};
}
void test()
{vector<string> a{ "张三", "李四", "王五", "赵六", "周七" };Matrix::Graph<string, int, false> g1(a);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.Print();
}
int main()
{test();return 0 ;
}2.2.邻接表的图实现
优势:查找顶点的度时(时间复杂度为O(1),添加一个计数),更节省空间;劣势:使用邻接表查找两个顶点是否有边且边的权值(最差情况:时间复杂度O(N)),插入效率低:需要遍历链表,看是否已存在
设计理念:有n个顶点,创建有n个元素的指针矩阵,插入一个新边 遍历链表看是否存在;
namespace List {template<class W>class Node {public:int _des;//权值W _weight;Node<W>* _next;Node(int des, W w):_des(des),_weight(w),_next(nullptr){}};template<class V, class W, bool Direction = false>class Graph{public:int Find(const V& v){auto it = _find_index.find(v);if (it == _find_index.end())return -1;return it->second;}bool AddEdge(const V& src, const V& des, const W& weight){//获取下标int si = Find(src);int di = Find(des);//不存在元素,fail;if (si == -1 || di == -1)return false;//邻接表添加边//数组指针是否为nullptrif (_table[si] == nullptr){//创建对象Node<W>* new_node = new Node<W>(di, weight);new_node->_next = _table[si];_table[si] = new_node;//无向图if (Direction == false) {Node<W>* new_node = new Node<W>(si, weight);new_node->_next = _table[di];_table[di] = new_node;}}else {//需要和邻接表内元素比较,是否已添加Node<W>* nd = _table[si];while (nd){if (nd->_des == di)return false;elsend = nd->_next;}//还未添加过Node<W>* new_node = new Node<W>(di, weight);new_node->_next = _table[si];_table[si] = new_node;//无向图if (Direction == false) {Node<W>* new_node = new Node<W>(si, weight);new_node->_next = _table[di];_table[di] = new_node;}}return true;}void Print(){for (int i = 0; i < _table.size(); i++){cout << _vertexs[i] << ": ";Node<W>* nd = _table[i];while (nd){cout << _vertexs[nd->_des] << " " << nd->_weight << " ";nd = nd->_next;}cout << endl;}}public:Graph(const vector<V>& v){int n = v.size();_vertexs.reserve(n);for (int i = 0; i < n; i++){_vertexs.push_back(v[i]);_find_index[v[i]] = i;}_table.resize(n, nullptr);}private://顶点集合vector<V> _vertexs;//顶点和下标的哈希unordered_map<V, int> _find_index;//邻接表vector<Node<W>*> _table;};
}
void test()
{vector<string> a{ "张三", "李四", "王五", "赵六", "周七" };List::Graph<string, int, false> g1(a);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.Print();
}
int main()
{test();return 0 ;
}2.3.图的DFS和BFS
我使用的是邻接表的图,来实现的,邻接矩阵也差不多,把代码插入List::graph类中就可以用了;
void _DFS(int pos, vector<bool>& visited){visited[pos] = true;Node<W>* nd = _table[pos];while (nd){cout << _vertexs[pos] << _vertexs[nd->_des] << " ";if (visited[nd->_des] == false)_DFS(nd->_des, visited);nd = nd->_next;}}void DFS(const V& v){int pos = _find_index[v];vector<bool> visited(_table.size(), false);_DFS(pos, visited);}void BFS(const V& v){int pos = _find_index[v];vector<bool> visited(_table.size(), false);queue<int> q;q.push(pos);while (!q.empty()){int size = q.size();while (size--){pos = q.front();visited[pos] = true;q.pop();Node<W>* nd = _table[pos];while (nd){cout << _vertexs[pos] << _vertexs[nd->_des] << " ";if (visited[nd->_des] == false)q.push(nd->_des);nd = nd->_next;}}}}
2.4.最小生成树
后续5种算法都使用Matrix::Graph类
最小生成树通常使用的都是无向图;
- 最小生成树:有n个顶点,使用n-1条边,使用所有顶点连通,那么肯定是不构成回路的(构成回路不可能所有连通);
2.4.1.Kruskal(克鲁斯卡尔算法)
贪心思想:
- 将所有边加入优先级队列;
- 拿出堆顶边(最小),使用并查集来判断是否构成回路;
- 每一条边都有两个顶点,将边的两个顶点使用并查集合并;
- 可能 不能构成最小生成树,所以结束条件为优先级队列不为空;
- 使用一个变量记录有多少边,最后为n-1条就是最小生成树;
并查集代码:在最上面
//贪心思想,选权值最小的边,使用并查集判断是否构成回路W Kruskal(Self& minTree){//初始化生成树int n = _vertexs.size();minTree._vertexs = _vertexs;minTree._find_index = _find_index;minTree._matrix.resize(n, vector<W>(n, W_MAX) );//优先级队列保存边priority_queue<Edge<W>, vector<Edge<W>>, greater<Edge<W>>> pq;//添加所有边进优先级队列for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){if (_matrix[i][j] != W_MAX)pq.push(Edge<W> (i, j, _matrix[i][j]) );}}//有n-1条边int count = 0;UnionFindSet<V> ufs(_vertexs);int totalW = 0;while (!pq.empty()){Edge<W> eg= pq.top();pq.pop();bool ret = ufs.Union(_vertexs[eg._src], _vertexs[eg._des]);if (ret == true){//不构成回路cout << _vertexs[eg._src] << ' ' << _vertexs[eg._des] << ' ' << eg._weight << endl;minTree.AddEdge(_vertexs[eg._src], _vertexs[eg._des], eg._weight);count++;totalW += eg._weight;}else {//cout << "构成环 " << _vertexs[eg._src] << ' ' << _vertexs[eg._des] << ' ' << eg._weight << endl;}//构成的总权值}if (count == n - 1)//能构成生成树return totalW;else//不能构成return W();}测试代码:

void TestGraphMinTree()
{const char* ch = "abcdefghi";vector<char> v;for (int i = 0; i < strlen(ch); i++){v.push_back(ch[i]);}Matrix::Graph<char, int> g(v);g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);Matrix::Graph<char, int> kminTree;cout << "Kruskal:" << g.Kruskal(kminTree) << endl;kminTree.Print();
}2.4.2.Prim(普里姆算法)
贪心思想:
- 确定一个顶点,将这个顶点的所有边加入优先级队列,这个顶点被设置为已使用;
- 拿出堆顶的边,看两个顶点是否已使用,已使用代表构环;
- 不构环将这个顶点的所有边,插入优先级队列,这个顶点被设置为已使用;
- 重复这个过程,我使用哈希表来判断顶点的,使用一个bool的数组应该更好;
- 使用一个变量记录有多少边,最后为n-1条就是最小生成树;
//贪心思想,按已选择的点延伸,使用set保存已使用,不使用使用过的就一定不会构环//不使用并查集是因为已使用节点都是连通的W Prim(Self &minTree, const V& val){int n = _vertexs.size();//初始化mintreeminTree._vertexs = _vertexs;minTree._find_index = _find_index;minTree._matrix.resize(n, vector<W>(n, W_MAX));int pos = _find_index[val];//保存已使用unordered_set<V> visited;visited.insert(pos);priority_queue<Edge<W>, vector<Edge<W>>, greater<Edge<W>> > pq;//for (int j = 0; j < n; j++) {if(_matrix[pos][j] != W_MAX)pq.push(Edge<W>(pos, j, _matrix[pos][j]));}int count = 0;//边数量W TotalW = 0;//权值大小while (!pq.empty()){//获取当前最小Edge<W> dg = pq.top();pq.pop();int des = dg._des;if(visited.count(des))//存在,不可用cout << "构成环 " << _vertexs[dg._src] << ' ' << _vertexs[dg._des] << ' ' << dg._weight << endl;else {for (int j = 0; j < n; j++)//添加新边{if(_matrix[des][j] != W_MAX)pq.push(Edge<W>(des, j, _matrix[des][j]));}visited.insert(des);//已使用minTree._matrix[dg._src][dg._des] = dg._weight;//生成树添边TotalW += dg._weight;count++;cout << _vertexs[dg._src] << ' ' << _vertexs[dg._des] << ' ' << dg._weight << endl;}}if (count == n - 1)return TotalW;elsereturn W();}测试代码:

void TestGraphMinTree()
{const char* ch = "abcdefghi";vector<char> v;for (int i = 0; i < strlen(ch); i++){v.push_back(ch[i]);}Matrix::Graph<char, int> g(v);g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);Matrix::Graph<char, int> kminTree;cout << "Prim:" << g.Prim(kminTree, 'a') << endl;kminTree.Print();
}2.5.最短路径
最短路径通常使用的都是有向图;
2.5.1.Dijkstra(迪杰斯特拉算法)
贪心思想:此算法的缺点:只能用做不带负权的图(负权就是小于0),因为不带负权已确定的路径值不可能更小(一个数加正数不可能更小);优势:性能最好(时间:O(N^2),邻接矩阵)
- 根据传入的顶点,将这个将他的路径值设为0;
- 进行遍历找到路径值最小且未使用的顶点,顶点设为已使用
- 遍历这个min顶点的所有边,如果这个min顶点路径值+这条边的值 < 目标顶点的路径值,更新目标顶点的路径值和 它的父亲为 这个min顶点;
- 循环此过程;
void Dijkstra(const V& v, vector<W>& dest, vector<int>& parentPath ){int n = _vertexs.size();//起始点下标int src = _find_index[v];//和初始点的最短路径dest.resize(n, W_MAX);//顶点父亲下标parentPath.resize(n, -1);dest[src] = W();//起始点置为0vector<bool> visited(n, false);//执行n次for (int i = 0; i < n; i++){int minW = W_MAX, minI = src;//找到当前最小顶点且未使用for (int j = 0; j < n; j++){if (visited[j] == false && dest[j] < minW){minI = j;minW = dest[j];}}//设为已使用的值,不可能更小visited[minI] = true;//延伸是否能找到更小顶点权值for (int j = 0; j < n; j++){//满足未使用,两个顶点右边if (visited[j] == false && _matrix[minI][j] != W_MAX){//新路径值更小if (dest[minI] + _matrix[minI][j] < dest[j]){//设置路径值和父顶点下标dest[j] = dest[minI] + _matrix[minI][j];parentPath[j] = minI;}}}}}测试代码:

void TestGraphDijkstra()
{const char* ch = "syztx";vector<char> v;for (int i = 0; i < strlen(ch); i++){v.push_back(ch[i]);}Matrix::Graph<char, int, true, INT_MAX > g(v);g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('y', 't', 3);g.AddEdge('y', 'x', 9);g.AddEdge('y', 'z', 2);g.AddEdge('z', 's', 7);g.AddEdge('z', 'x', 6);g.AddEdge('t', 'y', 2);g.AddEdge('t', 'x', 1);g.AddEdge('x', 'z', 4);vector<int> dest;vector<int> parentPath;g.Dijkstra('s', dest, parentPath);
}2.5.2.Bellman-Ford(贝尔曼-福特算法)
暴力思想:将邻接矩阵遍历n-1次;时间复杂度:O(N^3),优势:解决带负权的图问题
- 将传入的顶点的路径值设为0;
- 遍历整个邻接矩阵,当前顶点不为初始值且两者有边,当前顶点路径值 + 边的权值 < 目标顶点路径值,更新目标顶点的路径值和父亲;
- 遍历n - 1次,每个顶点最多有n - 1条边(除自己),如果一次遍历没有顶点路径值变小,结束循环;
- 如果带负权回路,可以无限小,没有结果,return false;
bool BellmanFord(const V& v, vector<W>& dest, vector<int>& parentPath){int n = _vertexs.size();int src = _find_index[v];//初始位置dest.resize(n, W_MAX);parentPath.resize(n, -1);//初始化初始位置dest[src] = 0;//为什么是n-1次:任意顶点到其他所有顶点最多n-1次,再多说明构成负权回路for (int k = 0; k < n - 1; k++){bool quit = true;//遍历权值邻接矩阵for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){//有边且本身不为初始值if (_matrix[i][j] != W_MAX && dest[i] != W_MAX && dest[i] + _matrix[i][j] < dest[j]){//设置更小的路径值和父顶点下标dest[j] = dest[i] + _matrix[i][j];parentPath[j] = i;quit = false;}}}if (quit)break;}//判断是否构成负权回路for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_matrix[i][j] != W_MAX && dest[i] != W_MAX && dest[i] + _matrix[i][j] < dest[j])return false;}}return true;}测试代码:

void TestGraphBellmanFord()
{const char* ch = "syztx";vector<char> v;for (int i = 0; i < strlen(ch); i++){v.push_back(ch[i]);}Matrix::Graph<char, int, true, INT_MAX> g(v);g.AddEdge('s', 't', 6);g.AddEdge('s', 'y', 7);g.AddEdge('y', 'z', 9);g.AddEdge('y', 'x', -3);g.AddEdge('z', 's', 2);g.AddEdge('z', 'x', 7);g.AddEdge('t', 'x', 5);g.AddEdge('t', 'y', 8);g.AddEdge('t', 'z', -4);g.AddEdge('x', 't', -2);vector<int> dist;vector<int> parentPath;if (g.BellmanFord('s', dist, parentPath)){}else{cout << "存在负权回路" << endl;}
}2.5.3.Floyd-Warshall(弗洛伊德算法)
动态规划思想:时间复杂度:O(N^3);可以算出所有节点为起始点的最短路径;
- 初始化路径值1.自己初始化为0 2.两顶点存在边初始化为边的权值;
- 顶点i 到 j 存在一个顶点k,满足Edge(i, k) + Edge(k, j) < Edge(i, j);说明有更小的路径值;
void FloydWarShall(vector<vector<W>>& vvDest, vector<vector<int>>& vvParentPath){int n = _vertexs.size();vvDest.resize(n);vvParentPath.resize(n);//初始化for (int i = 0; i < n; i++){vvDest[i].resize(n, W_MAX);vvParentPath[i].resize(n, -1);}//直接相连的顶点添加入二维数组for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_matrix[i][j] != W_MAX){vvDest[i][j] = _matrix[i][j];vvParentPath[i][j] = i;}else{vvParentPath[i][j] = -1;}if (i == j) {vvParentPath[i][j] = -1;vvDest[i][j] = 0;}}}//动规思想:i 到 j之间存在一个k,并且i到k + k到j < i 到 jfor (int k = 0; k < n; k++){for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (vvDest[i][k] != W_MAX && vvDest[k][j] != W_MAX && vvDest[i][k] + vvDest[k][j] < vvDest[i][j]){vvDest[i][j] = vvDest[i][k] + vvDest[k][j];vvParentPath[i][j] = vvParentPath[k][j];}}}}}测试代码:
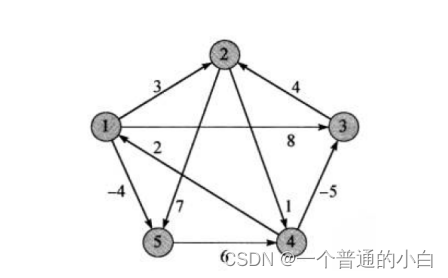
void TestFloydWarShall()
{const char* ch = "12345";vector<char> v;for (int i = 0; i < strlen(ch); i++){v.push_back(ch[i]);}Matrix::Graph<char, int, true, INT_MAX> g(v);g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);vector<vector<int>> vvDist;vector<vector<int>> vvParentPath;g.FloydWarShall(vvDist, vvParentPath);}