wordpress整站备份合肥竞价推广
项目场景:
提示:这里简述项目背景:
场景如下: java 项目运行时,后端控制台出现如下图所示报错信息: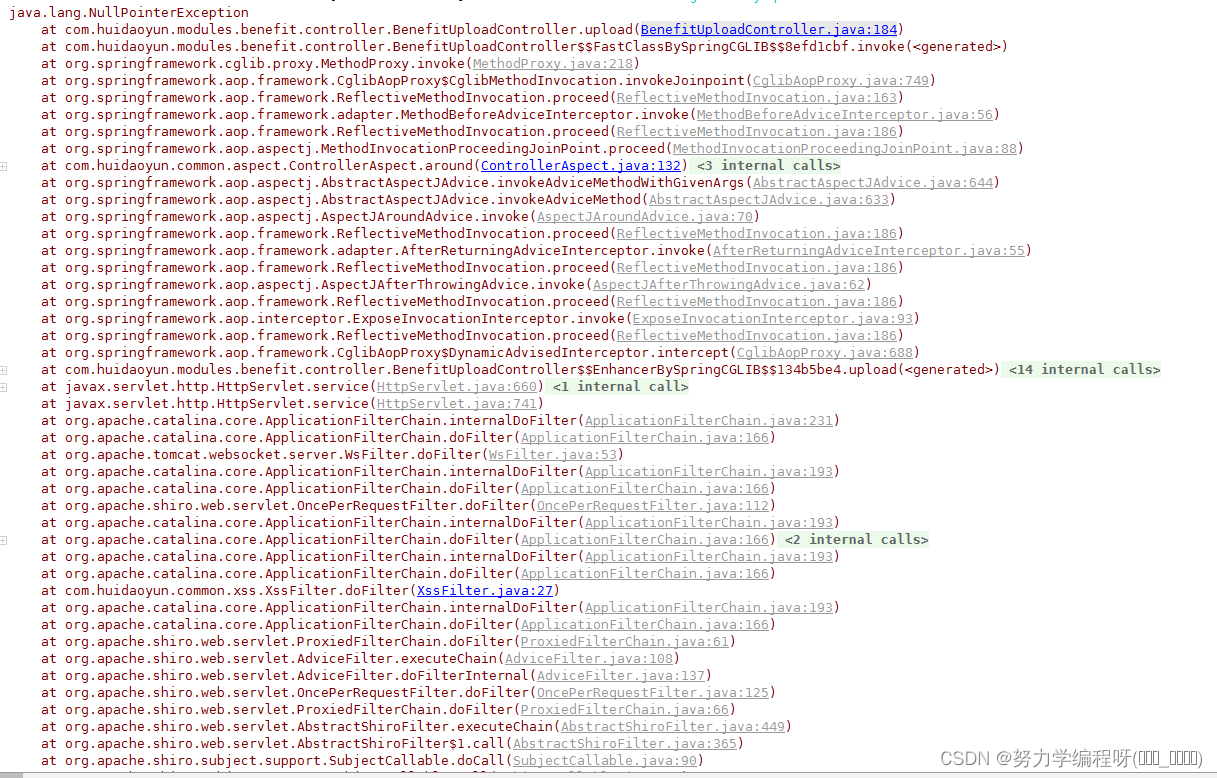 —
—
问题描述
提示:这里描述项目中遇到的问题:
java 项目运行时,后端控制台出现如下所示报错信息: 空指针异常
java.lang.NullPointerExceptionat com.huidaoyun.modules.benefit.controller.BenefitUploadController.upload(BenefitUploadController.java:184)at com.huidaoyun.modules.benefit.controller.BenefitUploadController$$FastClassBySpringCGLIB$$8efd1cbf.invoke(<generated>)at org.springframework.cglib.proxy.MethodProxy.invoke(MethodProxy.java:218)at org.springframework.aop.framework.CglibAopProxy$CglibMethodInvocation.invokeJoinpoint(CglibAopProxy.java:749)at org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:163)at org.springframework.aop.framework.adapter.MethodBeforeAdviceInterceptor.invoke(MethodBeforeAdviceInterceptor.java:56)at org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)at org.springframework.aop.aspectj.MethodInvocationProceedingJoinPoint.proceed(MethodInvocationProceedingJoinPoint.java:88)at com.huidaoyun.common.aspect.ControllerAspect.around(ControllerAspect.java:132)at sun.reflect.GeneratedMethodAccessor196.invoke(Unknown Source)at sun.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)at java.lang.reflect.Method.invoke(Method.java:498)at org.springframework.aop.aspectj.AbstractAspectJAdvice.invokeAdviceMethodWithGivenArgs(AbstractAspectJAdvice.java:644)at org.springframework.aop.aspectj.AbstractAspectJAdvice.invokeAdviceMethod(AbstractAspectJAdvice.java:633)at org.springframework.aop.aspectj.AspectJAroundAdvice.invoke(AspectJAroundAdvice.java:70)at org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)at org.springframework.aop.framework.adapter.AfterReturningAdviceInterceptor.invoke(AfterReturningAdviceInterceptor.java:55)at org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)at org.springframework.aop.aspectj.AspectJAfterThrowingAdvice.invoke(AspectJAfterThrowingAdvice.java:62)at org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)at org.springframework.aop.interceptor.ExposeInvocationInterceptor.invoke(ExposeInvocationInterceptor.java:93)at org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)at org.springframework.aop.framework.CglibAopProxy$DynamicAdvisedInterceptor.intercept(CglibAopProxy.java:688)at com.huidaoyun.modules.benefit.controller.BenefitUploadController$$EnhancerBySpringCGLIB$$134b5be4.upload(<generated>)at sun.reflect.NativeMethodAccessorImpl.invoke0(Native Method)at sun.reflect.NativeMethodAccessorImpl.invoke(NativeMethodAccessorImpl.java:62)at sun.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)at java.lang.reflect.Method.invoke(Method.java:498)at org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:189)at org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:138)at org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:102)at org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod(RequestMappingHandlerAdapter.java:895)at org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal(RequestMappingHandlerAdapter.java:800)at org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)at org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1038)at org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:942)at org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1005)at org.springframework.web.servlet.FrameworkServlet.doPost(FrameworkServlet.java:908)at javax.servlet.http.HttpServlet.service(HttpServlet.java:660)at org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:882)at javax.servlet.http.HttpServlet.service(HttpServlet.java:741)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:231)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.apache.shiro.web.servlet.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:112)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.web.filter.CorsFilter.doFilterInternal(CorsFilter.java:96)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at com.huidaoyun.common.xss.XssFilter.doFilter(XssFilter.java:27)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.apache.shiro.web.servlet.ProxiedFilterChain.doFilter(ProxiedFilterChain.java:61)at org.apache.shiro.web.servlet.AdviceFilter.executeChain(AdviceFilter.java:108)at org.apache.shiro.web.servlet.AdviceFilter.doFilterInternal(AdviceFilter.java:137)at org.apache.shiro.web.servlet.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:125)at org.apache.shiro.web.servlet.ProxiedFilterChain.doFilter(ProxiedFilterChain.java:66)at org.apache.shiro.web.servlet.AbstractShiroFilter.executeChain(AbstractShiroFilter.java:449)at org.apache.shiro.web.servlet.AbstractShiroFilter$1.call(AbstractShiroFilter.java:365)at org.apache.shiro.subject.support.SubjectCallable.doCall(SubjectCallable.java:90)at org.apache.shiro.subject.support.SubjectCallable.call(SubjectCallable.java:83)at org.apache.shiro.subject.support.DelegatingSubject.execute(DelegatingSubject.java:387)at org.apache.shiro.web.servlet.AbstractShiroFilter.doFilterInternal(AbstractShiroFilter.java:362)at org.apache.shiro.web.servlet.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:125)at org.springframework.web.filter.DelegatingFilterProxy.invokeDelegate(DelegatingFilterProxy.java:357)at org.springframework.web.filter.DelegatingFilterProxy.doFilter(DelegatingFilterProxy.java:270)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.boot.actuate.web.trace.servlet.HttpTraceFilter.doFilterInternal(HttpTraceFilter.java:90)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.web.filter.RequestContextFilter.doFilterInternal(RequestContextFilter.java:99)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.web.filter.FormContentFilter.doFilterInternal(FormContentFilter.java:92)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.web.filter.HiddenHttpMethodFilter.doFilterInternal(HiddenHttpMethodFilter.java:93)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:117)at org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal(WebMvcMetricsFilter.java:106)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal(CharacterEncodingFilter.java:200)at org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107)at org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:193)at org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:166)at org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:200)at org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:96)at org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:490)at org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:139)at org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)at org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:74)at org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:343)at org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:408)at org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:66)at org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:834)at org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1415)at org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49)at java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1142)at java.util.concurrent.ThreadPoolExecutor$Worker.run(ThreadPoolExecutor.java:617)at org.apache.tomcat.util.threads.TaskThread$WrappingRunnable.run(TaskThread.java:61)at java.lang.Thread.run(Thread.java:745)
原因分析:
分析问题:
首先我们考虑下 出现空指针异常可能的几种原因:
1、未初始化变量,变量的值为 null
2、获取到的参数为空,即当一个对象的值为空时,使用时没有先进行判断为空,直接使用。
3、接口类型的对象没有用具体的类初始化。
4、变量、数组 、或集合为进行初始化或 获取到的值为 null ,但在代码中直接进行使用
4、字符串与文字的比较,注意比较时 使用 .equals() 方法,但需注意的是 “ ”
和 null 及 ‘ ’ 是有区别的。
5、变量类型需要转为 string 类型使用时,优先使用String.valueOf()方法代替toString()
解决方案:
解决方法:
通过代码分析发现,是由于 获取到的值 为 null ,但是代码中未先进行空值判断,直接使用该变量,导致运行时前端未传值时报空指针异常的错误。
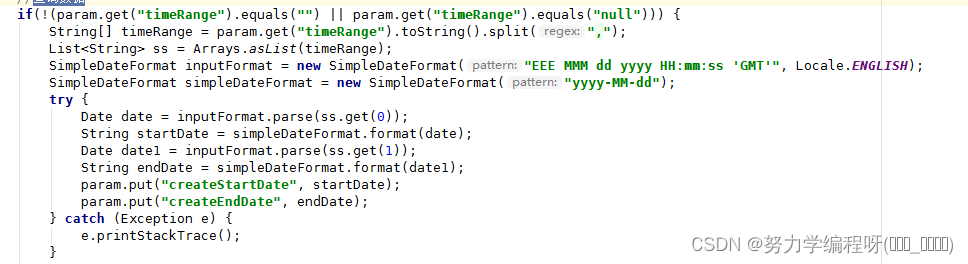
需 对变量进行空值判断,不为空时再对变量进行相应的处理,这样就会 避免 空指针异常的 出现了。
