企业做pc网站需要什么资料深圳华强北在哪个区
目录
测试工作中常用到的测试桩mock能力
应用场景
简单测试桩
http.server扩展:一行命令实现一个静态文件服务器
性能优化:使用异步响应
异步响应
能优化:利用多核
gunicorn
安装 gunicorn
使用 gunicorn 启动服务
性能优化:使用缓存(functools.lru_cache)。
单元测试中的mock
Python unittest.mock
总结
资料获取方法
测试工作中常用到的测试桩mock能力
在我们的测试工作过程中,可能会遇到前端服务开发完成,依赖服务还在开发中;或者我们需要压测某个服务,而这个服务的依赖组件(如测试环境MQ) 无法支撑并发访问的场景。这个时候我们可能就需要一个服务,来替代测试环境的这些依赖组件或服务,而这就是本文的主角--测试桩。
测试桩可以理解为一个代理,它可以用于模拟应用程序中的外部依赖项,如数据库、网络服务或其他API,它可以帮助我们在开发和测试过程中隔离应用程序的不同部分,从而使测试更加可靠和可重复。
应用场景
测试桩使用的一般有以下几种场景:
| 场景 | 使用测试桩的原因与目的 |
|---|---|
| 单元测试 | 隔离被测代码与其他组件或外部依赖的交互,便于在不考虑其他部分的情况下对被测代码进行测试。 |
| 集成测试 | 当某些组件未实现或不可用时,使用测试桩模拟这些组件,以便继续进行集成测试。 |
| 性能测试 | 快速生成高负载和大量并发请求,评估系统在高负载条件下的性能表现。 |
| 故障注入和恢复测试 | 模拟故障(如网络故障、服务宕机等),验证系统在遇到故障时的行为和恢复能力。 |
| API测试 | 使用测试桩模拟API的响应,以便在API实现完成之前就可以进行客户端开发和测试。 |
| 第三方服务测试 | 在开发和测试阶段避免与真实的第三方服务进行交互,降低额外成本和不稳定的测试结果。测试桩用于模拟这些第三方服务,使得在不影响真实服务的情况下进行测试。 |
本文将选取常用的几个场景循序渐进地介绍测试桩的开发和优化。
简单测试桩
如果在测试环境中不方便安装其他的库,我们可以使用Python标准库中的一个模块http.server模块创建一个简单的HTTP请求测试桩。
# simple_stub.py
# 测试桩接收GET请求并返回JSON数据。
import json
from http.server import BaseHTTPRequestHandler, HTTPServerclass SimpleHTTPRequestHandler(BaseHTTPRequestHandler):def do_GET(self):content = json.dumps({"message": "Hello, this is a test stub!"}).encode("utf-8")self.send_response(200)self.send_header("Content-Type", "application/json")self.send_header("Content-Length", f"{len(content)}")self.end_headers()self.wfile.write(content)if __name__ == "__main__":server_address = ("", 8000)httpd = HTTPServer(server_address, SimpleHTTPRequestHandler)print("Test stub is running on port 8000")httpd.serve_forever()
运行上面的代码,将看到测试桩正在监听8000端口。您可以使用浏览器或curl命令访问 http://localhost:8000,将会收到 {'message': 'Hello, this is a test stub!'}的响应。
http.server扩展:一行命令实现一个静态文件服务器
http.server模块可以作为一个简单的静态文件服务器,用于在本地开发和测试静态网站。要启动静态文件服务器,请在命令行中运行以下命令:
python3 -m http.server [port]
其中[port]是可选的端口号,不传递时默认为8000。服务器将在当前目录中提供静态文件。
如在日志文件夹中执行python -m http.server,就能在web浏览器中访问这个文件夹中的文件和子文件夹的内容:
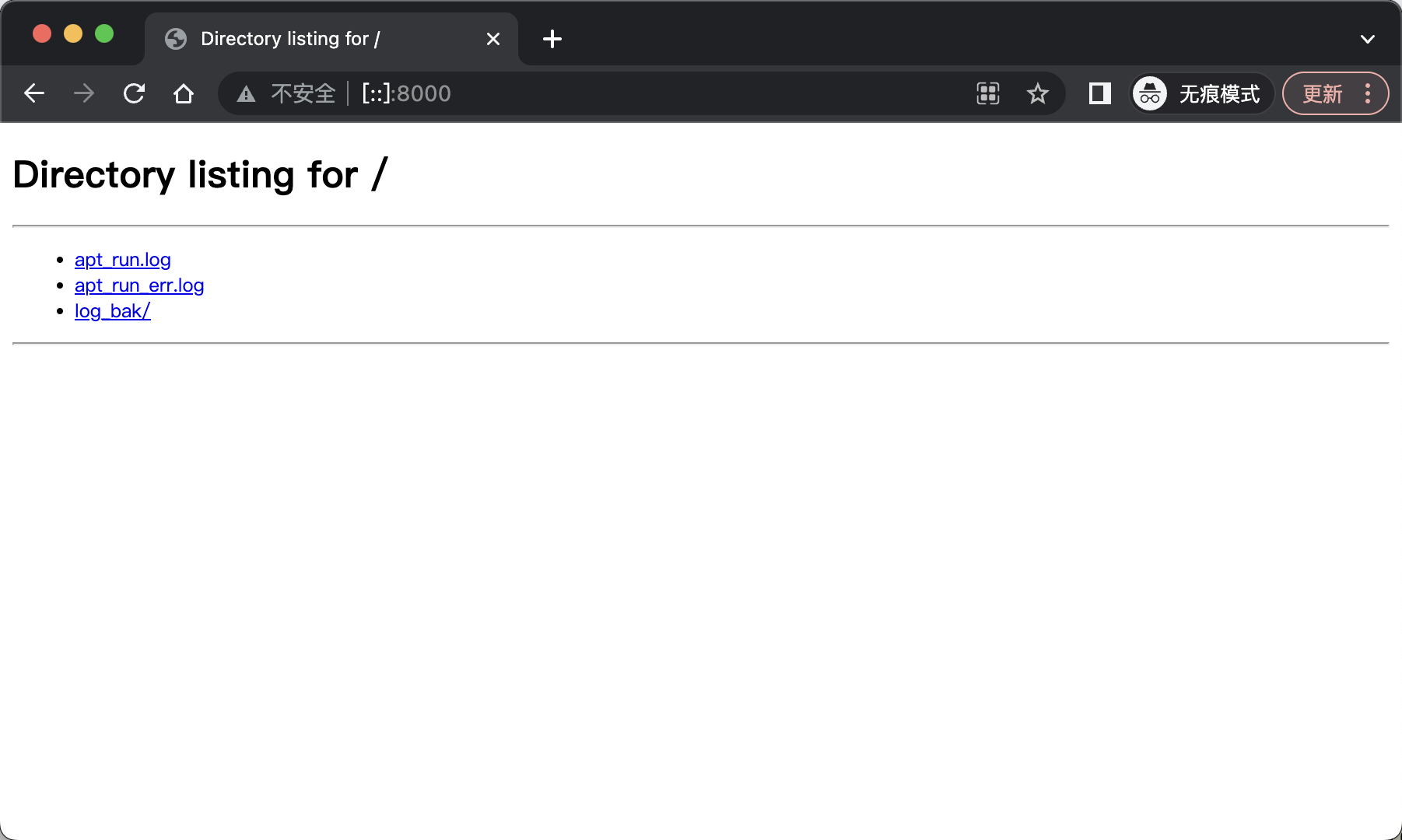
注意:
http.server主要用于开发和测试,性能和安全方面不具备在生产环境部署的条件
性能优化:使用异步响应
我们在前面的实现了一个简单的测试桩,但在实际应用中,我们可能需要更高的性能和更复杂的功能。
异步响应
在只有同样的资源的情况下,像这样的有网络I/O的服务,使用异步的方式无疑能更有效地利用系统资源。
说到异步的http框架,目前最火热的当然是FastAPI,使用FastAPI实现上面的功能只需两步。
首先,安装FastAPI和Uvicorn:
pip install fastapi uvicorn
接下来,创建一个名为fastapi_stub.py的文件,其中包含以下内容:
from fastapi import FastAPIapp = FastAPI()@app.get("/")
async def get_request():return {"message": "Hello, this is an optimized test stub!"}if __name__ == "__main__":import uvicornuvicorn.run(app, host="0.0.0.0", port=8000)
执行代码,这个测试桩也是监听在8000端口。我们可以像之前那样使用浏览器或其他HTTP客户端向测试桩发起请求。
点击查看异步编程优势 介绍
能优化:利用多核
虽然我们前面使用到了异步的方式来提升测试桩的性能,但是代码还是只是跑在一个CPU核心上,如果我们要进行性能压测,可能无法满足我们的性能需求。这个时候我们可以使用 gunicorn库 来利用上服务器的多核优势。
gunicorn
Gunicorn的主要特点和优势:
| 特点与优势 | 说明 |
|---|---|
| 简单易用 | Gunicorn易于安装和配置,可以与许多Python Web框架(如Flask、Django、FastAPI等)无缝集成。 |
| 多进程 | Gunicorn使用预先分叉的工作模式,创建多个子进程处理并发请求。这有助于提高应用程序的性能和响应能力。 |
| 兼容性 | Gunicorn遵循WSGI规范,这意味着它可以与遵循WSGI规范的任何Python Web应用程序一起使用。 |
| 可配置性 | Gunicorn提供了许多配置选项,如工作进程数量、工作进程类型(同步、异步)、超时设置等。这使得Gunicorn可以根据具体需求进行灵活配置。 |
| 部署友好 | Gunicorn在生产环境中非常受欢迎,因为它简化了部署流程。Gunicorn可以与其他工具(如Nginx、Supervisor等)一起使用,以便更好地管理和扩展Web应用程序。 |
安装 gunicorn
pip install gunicorn
使用 gunicorn 启动服务
启动服务:
gunicorn -w 4 fastapi_stub:app
可以看到,上面的命令启动了4个worker 进程,大家也可以使用ps -ef命令查询一下进程状态。
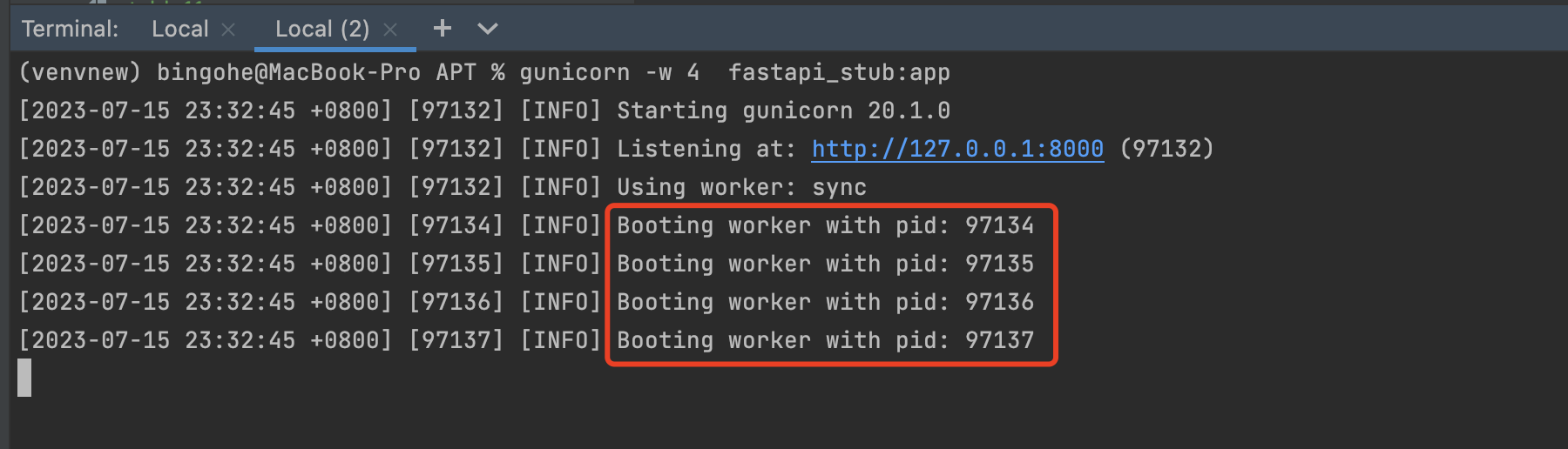
gunicorn的一些常用参数:
| 参数 | 说明 |
|---|---|
| -w, --workers | 设置工作进程的数量。根据系统的CPU核心数和应用程序的负载特征来调整。默认值为1。 |
| -k, --worker-class | 设置工作进程的类型。可以是sync(默认)、gevent、eventlet等。如果使用异步工作进程,需要安装相应的库。例如,对于FastAPI应用程序,可以使用-k uvicorn.workers.UvicornWorker。 |
| -b, --bind | 设置服务器绑定的地址和端口。格式为address:port。例如:-b 0.0.0.0:8000。默认值为127.0.0.1:8000。 |
| --timeout | 设置工作进程的超时时间(以秒为单位)。如果工作进程在指定的时间内没有完成任务,它将被重启。默认值为30秒。 |
| --log-level | 设置日志级别。可以是debug、info、warning、error或critical。默认值为info。 |
| --access-logfile | 设置访问日志文件的路径。默认情况下,访问日志将输出到标准错误流。要禁用访问日志,请使用-。例如:--access-logfile -。 |
| --error-logfile | 设置错误日志文件的路径。默认情况下,错误日志将输出到标准错误流。要禁用错误日志,请使用-。例如:--error-logfile -。 |
| --reload | 在开发环境中使用此选项,当应用程序代码发生更改时,Gunicorn将自动重新加载。不建议在生产环境中使用。 |
| --daemon | 使用此选项以守护进程模式运行Gunicorn。在这种模式下,Gunicorn将在后台运行,并在启动时自动分离。 |
Gunicorn提供了许多其他配置选项,可以根据具体需求进行调整。要查看完整的选项列表,可以查看Gunicorn的官方文档:https://docs.gunicorn.org/en/stable/settings.html。
性能优化:使用缓存(functools.lru_cache)。
当处理重复的计算或数据检索任务时。使用内存缓存(如Python的functools.lru_cache)或外部缓存(如Redis)来缓存经常使用的数据也能极大的提升测试桩的效率。
假设我们的测试桩需要使用到计算计算斐波那契数列这样耗时的功能,那么缓存结果,在下次遇到同样的请求时直接返回而不是先计算再返回,将极大的提高资源的使用率、减少响应的等待时间。
如果仅仅是直接返回数据的,没有进行复杂的计算的测试桩,使用
lru_cache并没有实际意义。
以下是一个更合适的使用lru_cache的示例,其中我们将对斐波那契数列进行计算并缓存结果:
from fastapi import FastAPI
from functools import lru_cacheapp = FastAPI()@lru_cache(maxsize=100)
def fibonacci(n: int):if n <= 1:return nelse:return fibonacci(n - 1) + fibonacci(n - 2)@app.get("/fibonacci/{n}")
async def get_fibonacci(n: int):result = fibonacci(n)return {"result": result}if __name__ == "__main__":import uvicornuvicorn.run(app, host="0.0.0.0", port=8000)
在这个示例中,我们使用FastAPI创建了一个简单的HTTP请求测试桩。我们定义了一个名为fibonacci的函数,该函数计算斐波那契数列。为了提高性能,我们使用functools.lru_cache对该函数进行了缓存。
在路由/fibonacci/{n}中,我们调用fibonacci函数并返回结果。可以命令访问 http://localhost:8000/fibonacci/{n}进行调试。
需要注意的是 maxsize参数是functools.lru_cache装饰器的一个配置选项,它表示缓存的最大容量。lru_cache使用字典来存储缓存项,当一个新的结果需要被缓存时,它会检查当前缓存的大小。如果缓存已满(即达到maxsize),则会根据LRU策略移除最近最少使用的缓存项。如果maxsize设置为None,则缓存可以无限制地增长,这可能导致内存问题。
单元测试中的mock
Python unittest.mock
在Python中,unittest模块提供了一个名为unittest.mock的子模块,用于创建mock对象。unittest.mock包含一个名为Mock的类以及一个名为patch的上下文管理器/装饰器,可以用于替换被测试代码中的依赖项。
import requests
from unittest import TestCase
from unittest.mock import patch# 定义一个函数 get_user_name,它使用 requests.get 发起 HTTP 请求以获取用户名称
def get_user_name(user_id):response = requests.get(f"https://api.example.com/users/{user_id}")return response.json()["name"]# 创建一个名为 TestGetUserName 的测试类,它继承自 unittest.TestCase
class TestGetUserName(TestCase):# 使用 unittest.mock.patch 装饰器替换 requests.get 函数@patch("requests.get")# 定义一个名为 test_get_user_name 的测试方法,它接受一个名为 mock_get 的参数def test_get_user_name(self, mock_get):# 配置 mock_get 的返回值,使其在调用 json 方法时返回一个包含 "name": "Alice" 的字典mock_get.return_value.json.return_value = {"name": "Alice"}# 调用 get_user_name 函数,并传入 user_id 参数user_name = get_user_name(1)# 使用 unittest.TestCase 的 assertEqual 方法检查 get_user_name 的返回值是否等于 "Alice"self.assertEqual(user_name, "Alice")# 使用 unittest.mock.Mock 的 assert_called_with 方法检查 mock_get 是否被正确调用mock_get.assert_called_with("https://api.example.com/users/1")
总结
在开发测试桩时,我们需要根据实际需求和后端服务的特点来设计测试桩的行为,为的是使其更接近实际后端服务的行为,确保测试结果具有更高的可靠性和准确性。
可能还有其他的优化方案,欢迎大家提出。希望本文能对大家的工作带来帮助。
如果觉得还不错,就在右下角点个赞吧,感谢!
资料获取方法
【留言777】


各位想获取源码等教程资料的朋友请点赞 + 评论 + 收藏,三连!
三连之后我会在评论区挨个私信发给你们~
