外国做挂的网站是多少钱手机网页在线
OPPO三面
一面(4.2,20min)
# 1.自我介绍# 2.三个项目,问的很详细
后面专门会出一版怎么做自我介绍,以及项目怎么写,会怎么问,你该怎么回答。
3.SPI是什么?有几条线?几种模式?
SPI协议简介
板卡内不同芯片间通讯最常用的三种串行协议:UART、I2C、SPI,之前写过串口协议及其FPGA实现,今天我们来介绍SPI协议,SPI是Serial Perripheral Interface的简称,是由Motorola公司推出的一种高速、全双工的总线协议。
与IIC类似,SPI也是采用主从方式工作,主机通常为FPGA、MCU或DSP等可编程控制器,从机通常为EPROM、Flash,AD/DA,音视频处理芯片等设备。
一般由SCLK、CS、MOSI,MISO四根线组成,有的地方可能是:SCK、SS、SDI、SDO等名称,都是一样的含义,当有多个从机存在时,通过CS来选择要控制的从机设备。
和标准SPI类似的协议,还有TI的SSP协议,区别主要在片选信号的时序上。
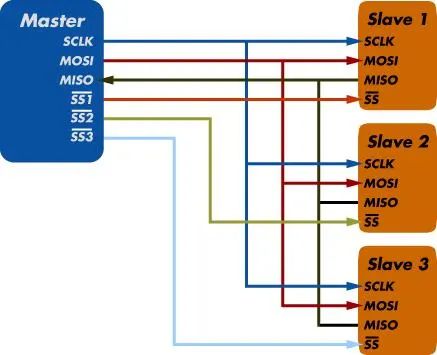
-
4线还是3线?<
