南通网站制作哪个好编程猫少儿编程app下载
一、业务需求及其痛点
大型企业需要对各种业务系统中的销售及营销数据进行实时同步分析,例如库存信息、对帐信号、会员信息、广告投放信息,生产进度信息等等,这些统计分析信息可以实时同步到StarRocks中进行分析和统计,StarRocks作为分析型数据库特别适合于对海量数据的存储和分析,我们只需要把MySQL的表单数据实时同步到StarRocks即可以实现实时数据分析能力。
二、StarRocks介绍
StarRocks 是一款极速全场景 MPP 企业级数据库产品,具备水平在线扩缩容,金融级高可用,兼容 MySQL 5.7 协议和 MySQL 生态,提供全面向量化引擎与多种数据源联邦查询等重要特性。StarRocks 致力于在全场景 OLAP 业务上为用户提供统一的解决方案,适用于对性能,实时性,并发能力和灵活性有较高要求的各类应用场景。
三、CDC实时同步工具选型
目前能免费使用的成熟CDC工具且同时支持MySQL+StarRocks的有Flink CDC和ETLCloud CDC等
这里我们主要考虑选择比较成熟的Flink CDC和ETLCloud CDC,CDC的同步原理其实不同平台的原理都是一样的,都是读取数据库log然后通过清洗、转换或计算后存入目标仓库中
Flink CDC安装和使用难度比较大,没有可视化的CDC配置和监控界面对于不熟的用户安装相对比较麻烦,对于实时数据的加工和处理还需要写代码,没一点技术的用户根据搞不定,对于数据工程师来说难度太大
ETLCloud CDC安装和使用相对容易提供了一键安装功能同时也支持windows个人电脑安装,安装完成后提供全WEB配置界面,对于用户可以说是非常友好,我们这里选择ETLCloud CDC来实现实时数仓的构建

四、怎么提升写入StarRocks的性能?
StarRocks兼容MySQL协议但是直接用jdbc写入StarRocks的速度是非常慢基本不可用,所以必须要采用StarRocks提供的Stream load方式来进行数据的载入才能提升速度
ETLCloud CDC提供了专门针对StarRocks的高性能输出组件,还支持自动创建表结构同时支持批量加载技术
五、数据写入StarRocks之前如何直接转换为宽表?
通常情况下我们使用CDC实时监听表销售或订单表数据的LOG时会形成流式的数据,CDC每次传入的数据有可能是一条也可能是多条,监听到的流式数据都是订单表的单条数据,但在业务上单表的数据在业务价值上可能缺少一些关键的维度业务数据字段,例如要计算毛利合并客户及产品数据等。
为了补充这些缺少的数据字段之前的做法是先让他入库,然后再用SQL语句或者ETL流程再给他变换一次形成我们需要的宽表数据,虽然这样也可以实现这个业务需求但是失去了数据处理的时效性,即本来是实时流的数据但是到了业务那里变成不是实时的了,因为我们中间有一个定时变换的数据过程。
通过ETLCloud的ETL功能可以轻松实现实时数据直接变为宽表数据存入到StarRocks中
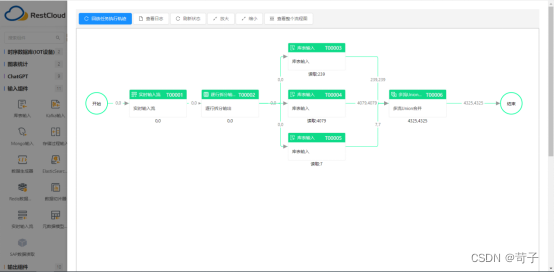
(单表实时流合并其他维度数据直接输出宽表数据到StarRocks中)
六、ETLCloud CDC同步原理
ETLCloud CDC的功能之所有比其他CDC工具都强大是因为他把CDC和ETL流程给链接起来了,CDC实时数据流入ETL流程中,再通过ETL流程对实时数据进行处理和输出。
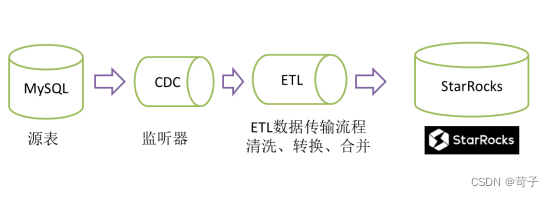
ETLCloud CDC中配置MySQL表的监听
MySQL先要开启bing log功能,开启方式可以查看
RestCloud 数据集成平台
开启动我们进入到ETLCloud的实时数据集成页面中配置一下即可
新增一个mysql cdc监听器
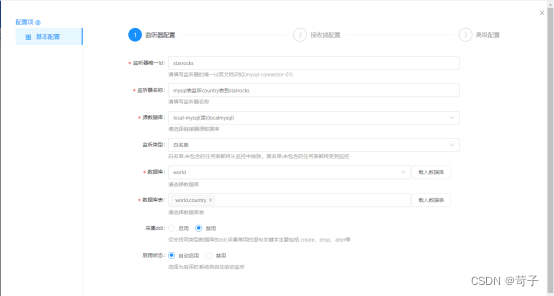
选择要监听mysql的表,这里我们选择监听country表
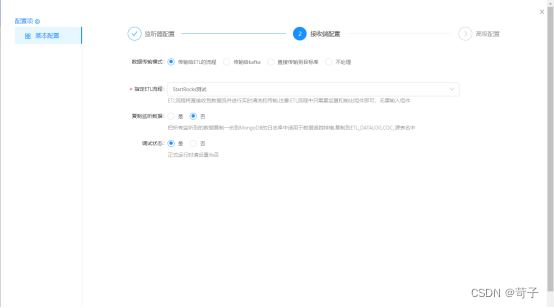
目标我们选择传给ETL的流程,ETL的流程会把数据写入到StarRocks中
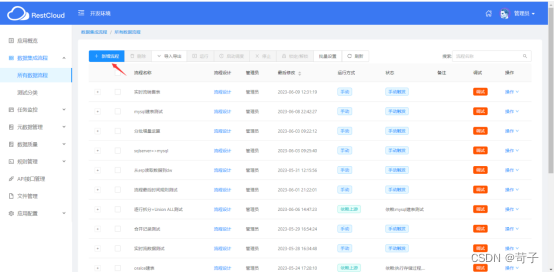
在离线集成中我们新建一个StarRocks输出的ETL流程
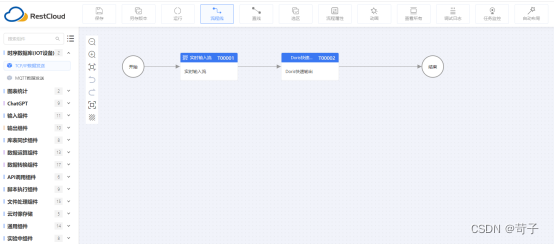
离线ETL流程很简单,只需要拉入一个StarRocks的输出组件即可
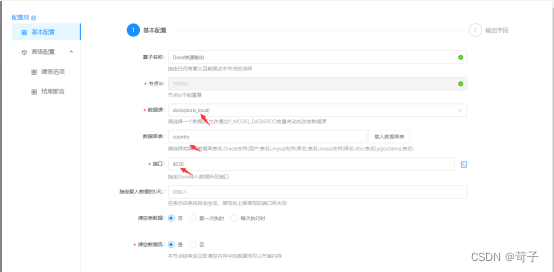
选中StarRocks数据源和StarRocks的数据库表,数据源在ETLCloud中已经提前建好
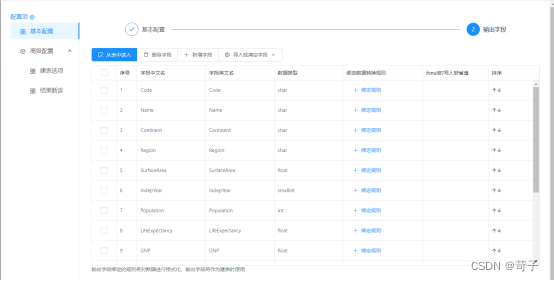
导入StarRocks表中的所有字段
这样CDC+ETL就完成了mysql=>StarRocks的实时同步任务的创建
启动MySQL CDC监听器
进入ETLCloud的实时数据集成功能点击启动CDC监听器即可
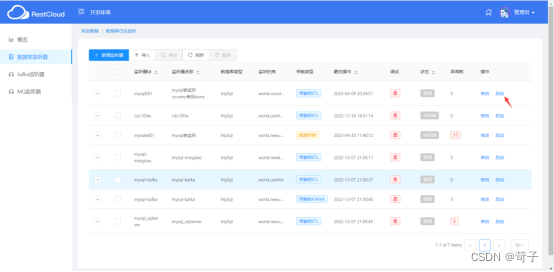
启动成功显示为绿色,如果出错可以查看tomcat log看是什么原因引起的
表示监听器已经启动成功
开始实时同步数据
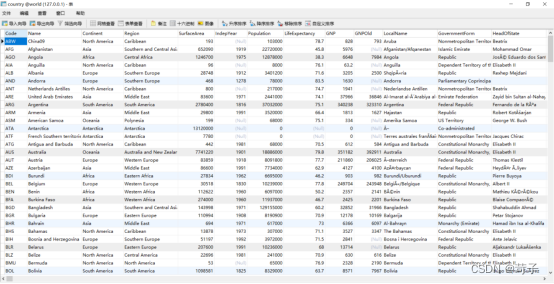
在mysql我们country表中的数据如下
我们可以随意修改其中几条数据,可以看到数据会立即同步到StarRocks中
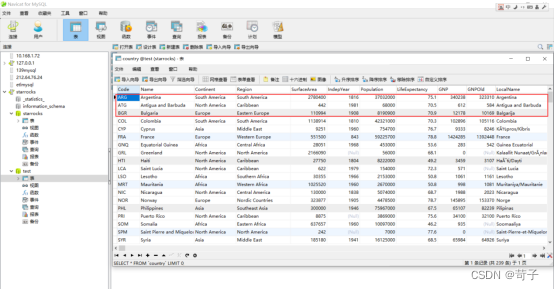
我们在mysql中实时修改了3条数据,可以看到StarRocks中已经立即有3条数据更新过来
同时我们也可以去观察ETL的离线流程是不是被CDC给调用了
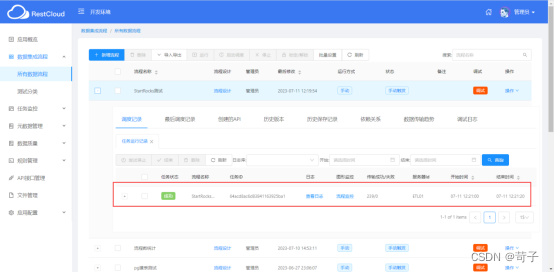
可以看到我们修改了3条数据,这个ETL流程被调用了1次,通过这个ETL流程把数据写入到了StarRocks中
StarRocks中自动建表
ETLCloud还具备在StarRocks中自动建表功能,如果我们要一次性把MySql的1000张表全部同步到StarRocks中,就可以使用批量同步功能,可以一次性把MySQL的1000张表自动在Doris中创建并全部同步数据到StarRocks中,这个也是Flink CDC所不具备的功能。
这们就可以把业务数据一次性全部拉入到StarRocks数仓中
StarRocks自动建表能力
