捕鱼网站建设网站开发的岗位与分工
作者:徽泠(苏墨馨)
为了庆祝 Grafana 的 10 年里程碑,Grafana Labs 推出了 Grafana 10,这个具有纪念意义的版本强调增强用户体验,使各种开发人员更容易使用。Grafana v10.0.x 为开发者与企业展示卓越的新功能、可视化与协作能力,其中还包括:
- 更新 Panel 面板
- 更新 Dashboard
- 更新导航栏
- 更新 Grafana Altering
本文仅介绍了 Grafana v10.0.x 更新的部分功能特性,更多详细信息,请参见 Grafana 官方文档 [ 1] 。
那么,今天我们带大家一一解读,Grafana 10 所带来的各种新特性与新能力。01
新的 Panel 面板
(1)XY Chart 面板
Grafana v10.0.x 支持新的 x-y 图表面板,包含折线图和散点图。

(2)XY Trend 面板
Grafana v10.0.x 新增 xy 趋势图,趋势图允许您展示 x 轴为数值(x 需要递增)而非时间的趋势。此面板解决了时间序列(Time Series)或 XY 图表面板(XY Chart)均无法解决的问题。例如,可以绘制函数图、rpm/ 扭矩曲线、供需关系等。

(3)DataGrid 面板
Grafana v10.0.x 新增 DataGrid 面板,支持在 Grafana 仪表板中编辑数据来自定义数据,您可以用于微调从数据源读取的数据或者用于创建新的数据。
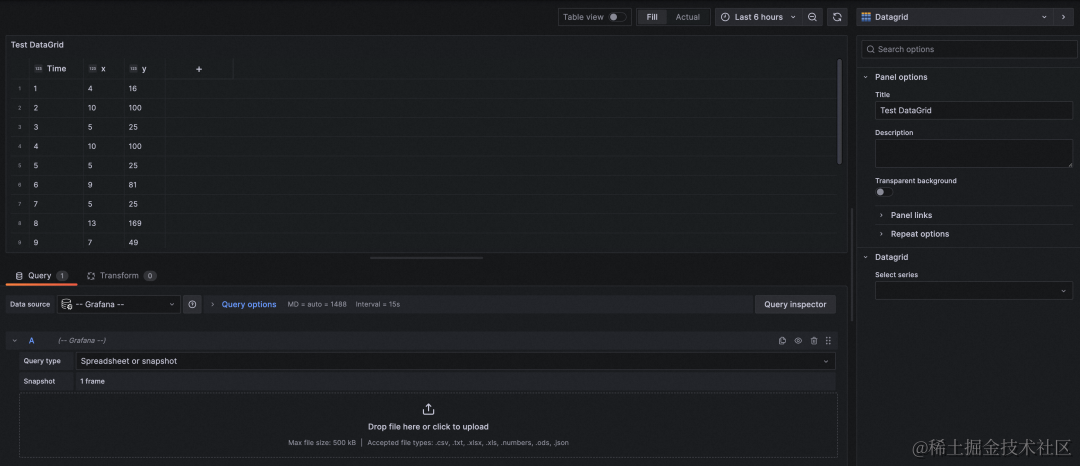

修改后的数据以快照的形式保存,不随时间更新。
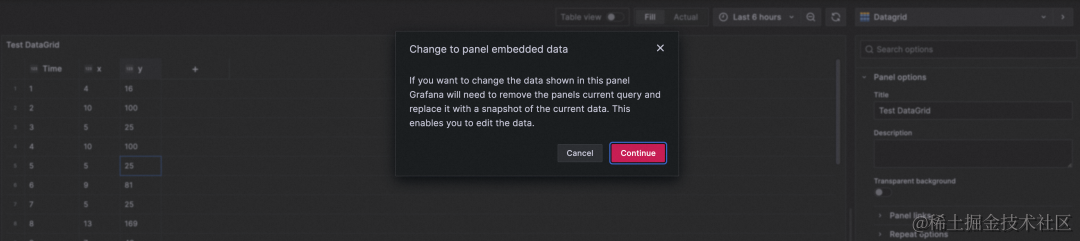
保存 DataGrid 之后,在新的 panel 里选择 dashboard 数据源,可以用微调后的数据作为数据源,并支持对 DataGrid 数据进行 transform。
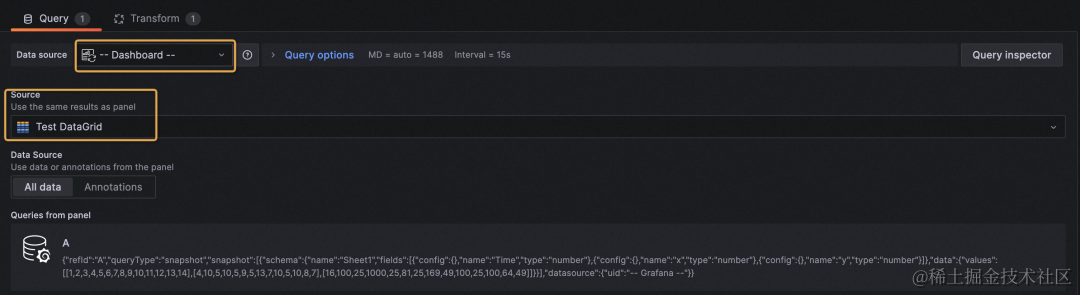
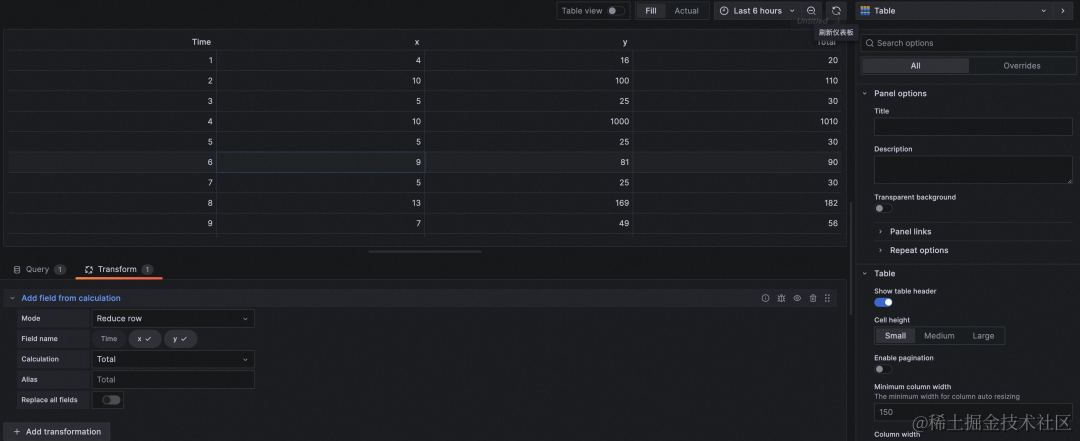
(4)Canvas 面板
Canvas 是一个新面板,它将 Grafana 的强大功能与自定义元素的灵活性相结合。画布可视化是可扩展的 form-built 面板,允许用户在静态和动态布局中显式放置元素,从而以标准 Grafana 面板无法实现的方式设计自定义可视化和叠加数据。例如,您可以放置图像图层,然后叠加由 Grafana 数据源更新的文本,并显示可以根据数据有条件地更改颜色的图标。


(5)Logs Panel 面板优化
Grafana v10.0.x 对 Logs 类型的展示做了进一步的优化,新增以下功能或组件:
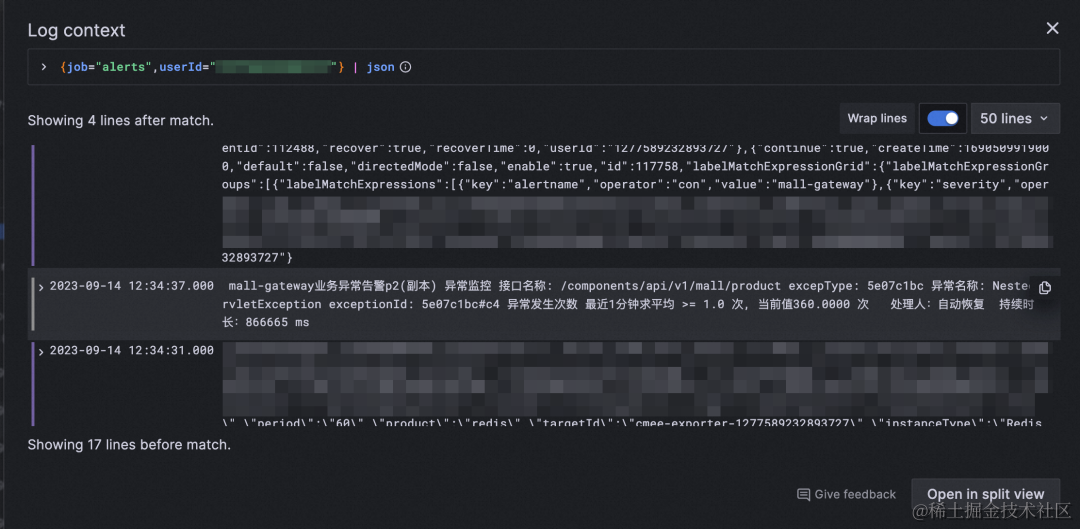
- 通过操作记录详细信息,包括用于轻松复制行的“复制”按钮,以及用于仅显示选定标签的眼睛图标,使用户可以专注于特定信息,而无需离开日志上下文部分。
- 换行切换可自动换行长文本,以便于直接在日志上下文中阅读和分析日志条目上下文。
- “在拆分视图中打开”按钮,用于在 Explore 的拆分屏幕中执行日志条目的上下文查询。
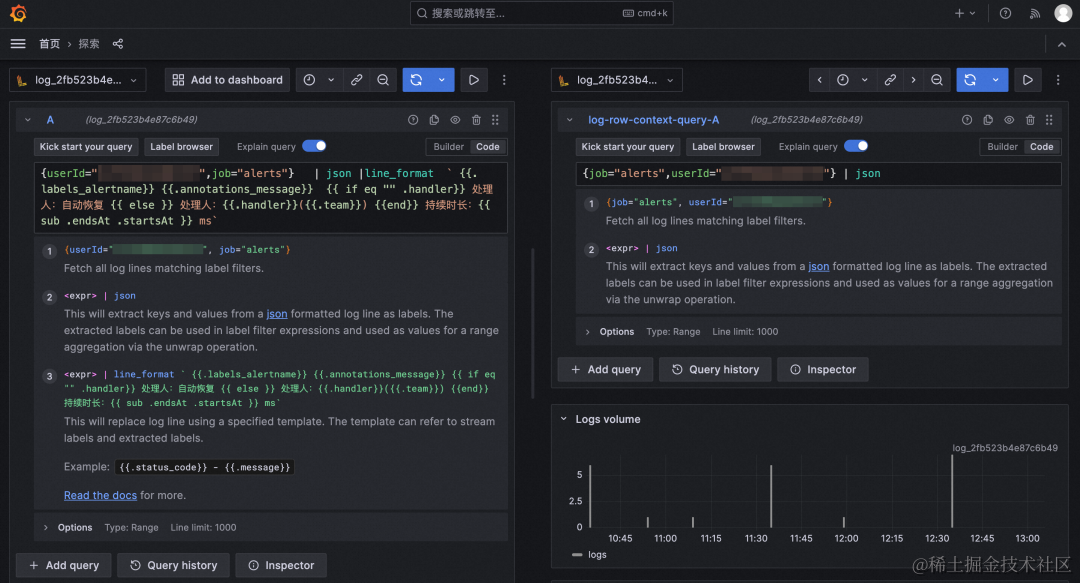
a. 支持直接复制日志内容&长文本展开

b. 选中的 log 前后的 context 展开,可以直接分屏。
新的 dashboard
(1)多级文件夹
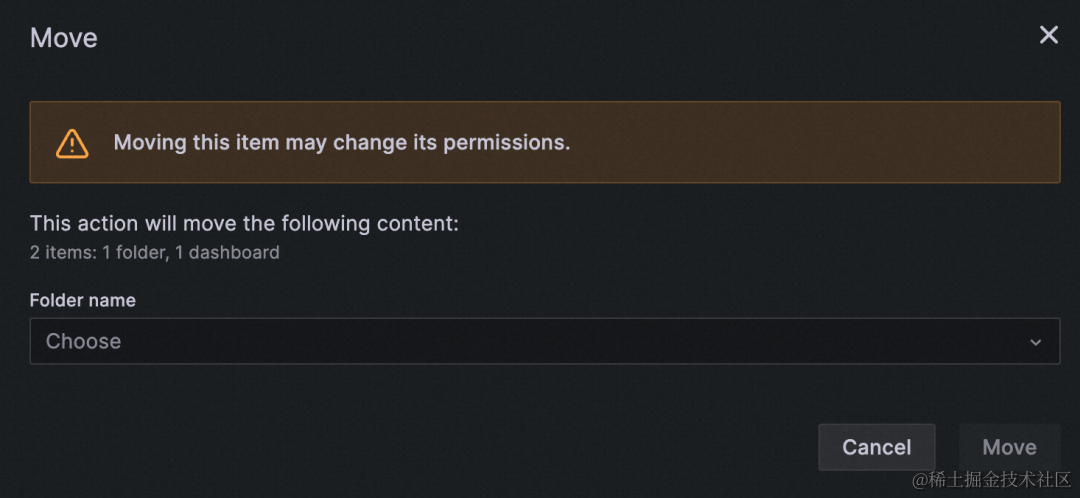
Grafana v10.0.x 支持多级文件夹,便于对大量仪表盘更有层次地进行管理。
注意: 子文件夹移动的时候会继承新的父文件夹的权限。

(2)支持混合数据源的查询
Grafana v10.0.x 的 Explore 中选择 Mixed 数据源可以为每一个查询定义一个数据源,展示在同一个图里。

(3)数据源选择
- Grafana v10.0.x 在选择数据源的时候,点击 open advanced datasource picker 展开数据源选择页面,更清晰的展示可选数据源。
- Grafana v10.0.x 编辑面板或者创建面板的时候,在数据源选择页面可以通过拖拽或者选择上传特定类型的数据源,如 .csv, .txt, .xlsx, .json 等。

(4)注释->时间区域标记及筛选
Grafana10 支持时间序列(time series)面板时间区域的标记。时间区域提供了更加情境化的体验,能够突出显示一周中的某些日子,例如周一至周五,以在数据旁边显示工作周。时间区域也是突出显示一天中特定部分(例如夜间、工作时间或想要为每天定义的任何内容)的有用方法。它们可以让用户快速定位一天中的某些部分或忽略时间序列中突出显示的部分。
设置方法: 在仪表盘的设置里的 annotations 里创建需要应用的注释,应用即可。

以上注释的效果为每天的 15:00-19:00 特殊标注:

可以根据需要定义不同的时间区域展示:

可以过滤仪表板注释以将注释应用到所有面板或选定的面板,或使用它们排除选定的面板。

更新导航栏
(1)搜索栏
Grafana v10.0.x 所有页面的顶部都加了搜索栏,可以直接搜索和访问所有页面和最近使用的仪表板。
(2)数据源连接(connections)
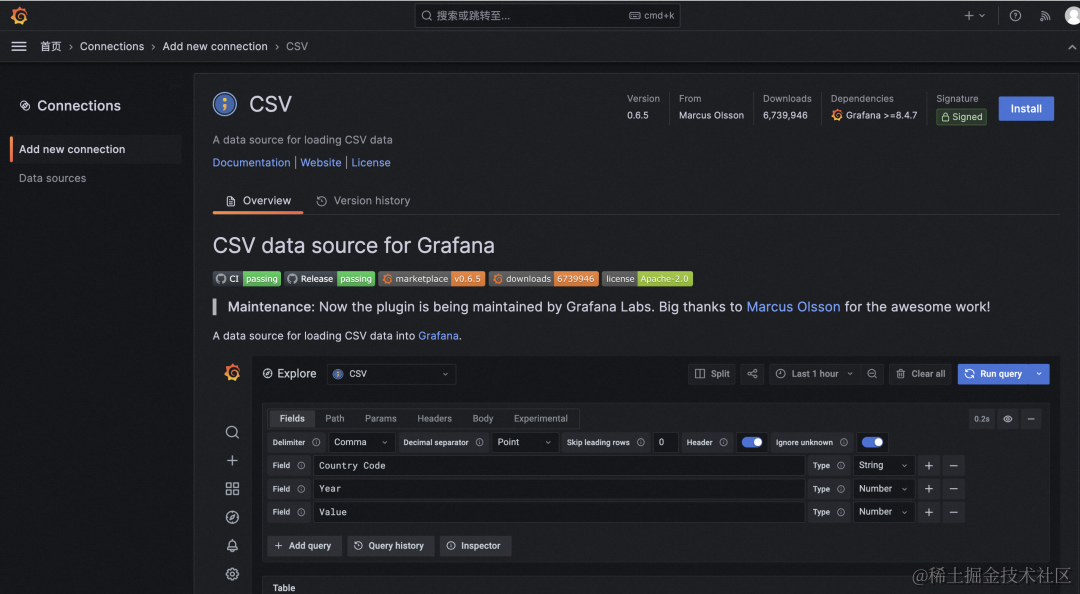
Grafana v10.0.x 左侧导航中的 connections 提供了新的数据源创建和编辑路径,将数据源相关工具组合在一起以便于访问。
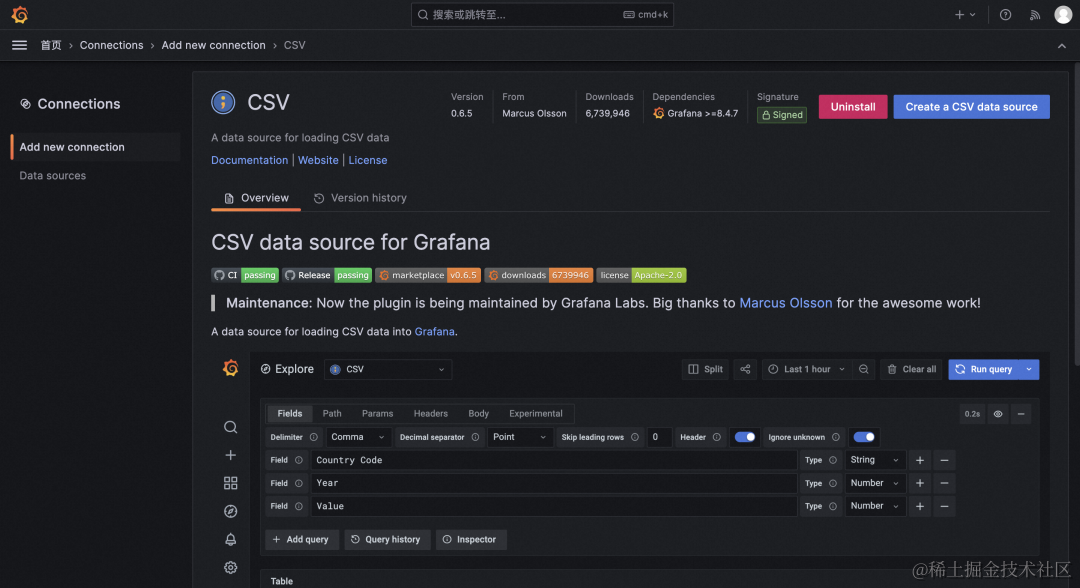
Add new connection 展示所有数据源插件,install 之后直接通过插件的页面就可以创建数据源。
Data sources 和 Grafana 9 管理数据源一致。
注意: install 需要用 admin 登录。
Grafana 10 仍旧支持旧的数据源安装路径,但会有提醒。

(3)页面跳转
通过 breadcrumb 组件显示当前页面的路径,快速返回之前路径上的任意页面。

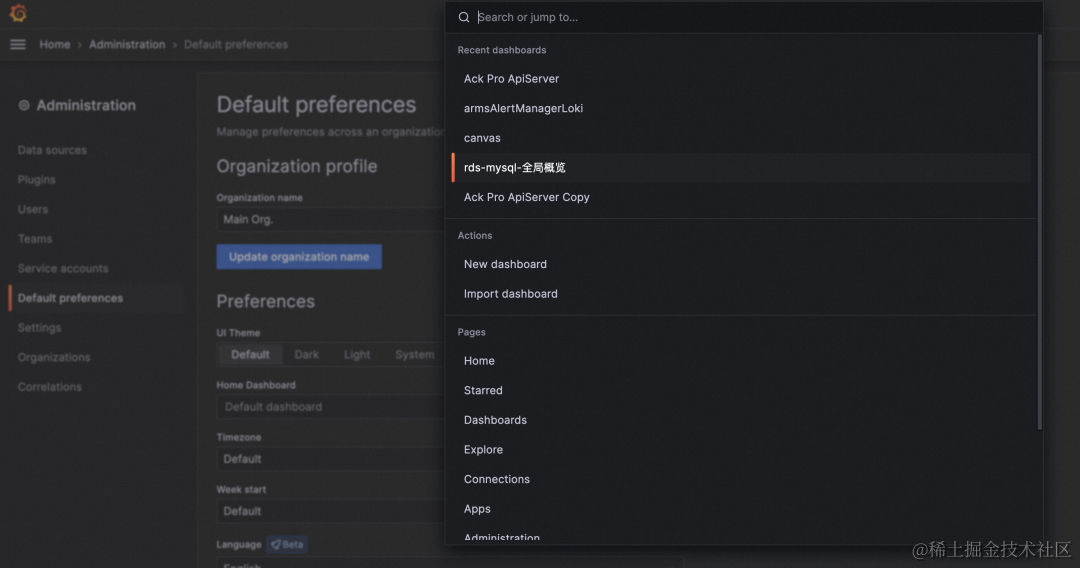
(4)中文支持
Grafana v10.0.x 在 administration-> default preference 里新增语言设置,支持中文。

更新 Grafana Altering 告警
(1)预览通知模版
Grafana 10 定义告警通知模版后可以预览告警的内容。

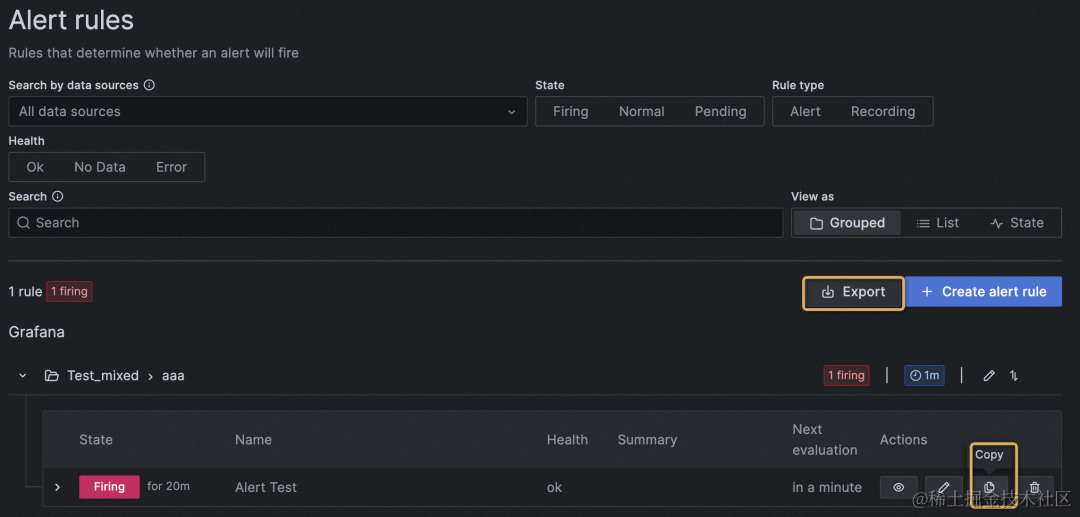
(2)复制创建新的告警规则
通过复制可以创建新的告警规则,在需要多个相似规则时可以更便捷的进行创建。
支持通过 export 导出全部告警规则。
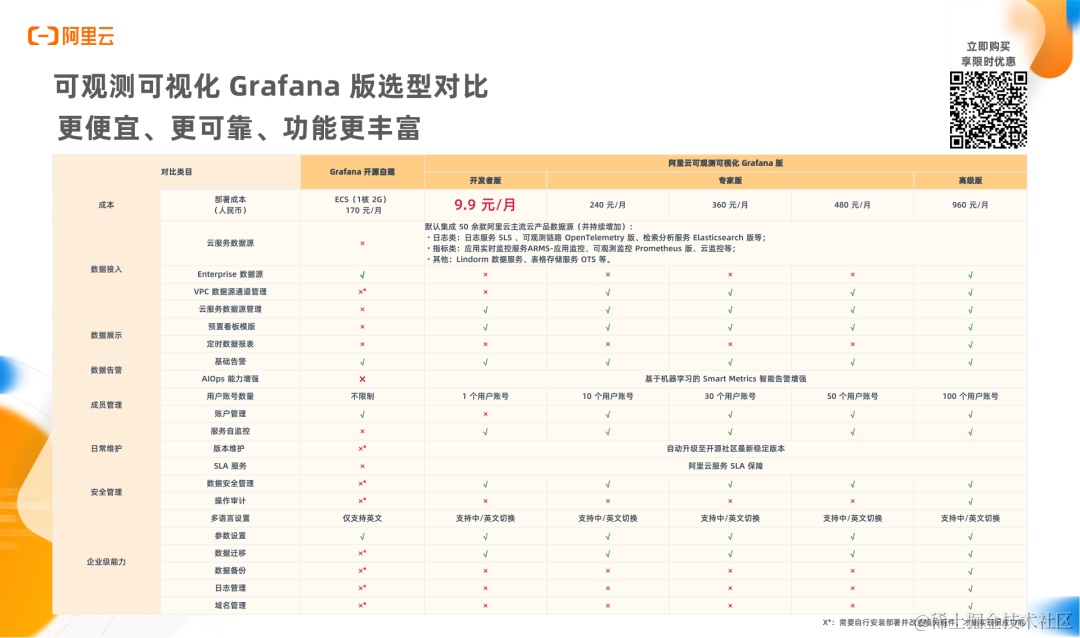
开源 Grafana 对比,阿里云可观测可视化 Grafana 版
相较于开源版本,阿里云可观测可视化 Grafana 版目前已支持 10.x 稳定版本。同时,结合不同用户群体的实际需求,提供不同规模的 Grafana 托管服务,为开发者与企业进一步降低 Grafana 的使用成本。最低规格的开发者版本每月仅需 9.9 元, 免去自建时的 ECS 运维成本与数据集成问题。
与此同时,可观测可视化 Grafana 版已加入阿里云免费试用计划,提供 10U 专家版免费试用一个月。
相关链接:
[1] Grafana 官方文档****
https://grafana.com/docs/grafana/latest/whatsnew/whats-new-in-v10-0/
