高古楼网站 做窗子seo关键词优化推广报价表
提起PS后期修图人像美白磨皮,大家会想到各种磨皮工具,其中Portraiture这款磨皮效率超高,是99%摄影师的必备插件,一秒磨皮,无卡顿,效果好!人像摄影师人均一款,磨皮质感非常好,不失真,如果你能够熟练掌握的话,里面很多功能完全可以替代双曲线高低频磨皮!一键磨皮效果更有质感,对皮肤识别能力更强,效果远超老版本插件!
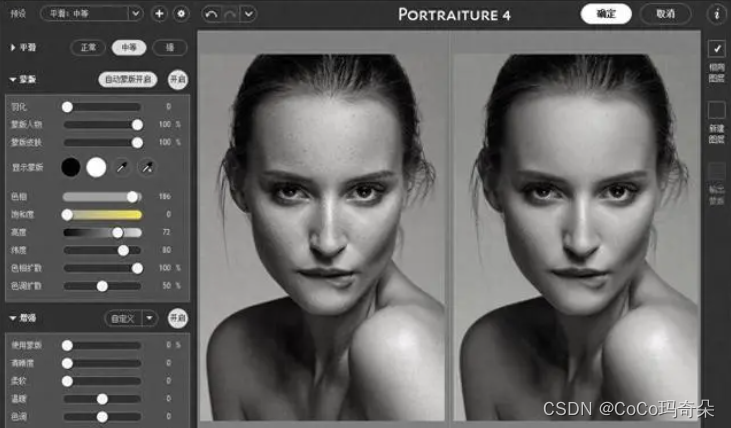
该插件包含了一系列智能滤镜和工具,让用户能够自动化和简化人像照片修改的过程。以下是 Portraiture 4 提供的主要功能:
人脸识别:Portraiture 4 使用智能算法准确识别人脸,并自动应用修饰效果,无需手动选取区域。
肤色优化:插件内置了丰富的肤色调整工具,可以平衡和改善肤色的颜色、纹理和光泽度,使皮肤看起来更加光滑和自然。
瑕疵修复:Portraiture 4 能够检测并自动修复人像照片中的皮肤瑕疵,如斑点、痘痘和皱纹等。
写实效果:该插件还提供了多种写实效果的调整工具,如锐化、增加细节和改善对比度等,以增强照片的质感和细节。
自定义设置:用户可以根据需要自定义调整滤镜的强度、效果和应用范围,以满足不同照片和个人风格的需求。
Portraiture for Photoshop win-安装包下载如下:
https://wm.makeding.com/iclk/?zoneid=50180
Portraiture for Photoshop mac-安装包下载如下:
https://wm.makeding.com/iclk/?zoneid=45781
Portraiture for Lightroom win-安装包下载如下:
https://wm.makeding.com/iclk/?zoneid=54577
Portraiture for Lightroom mac-安装包下载如下:
https://wm.makeding.com/iclk/?zoneid=54578
用户量向我们证明了强大的手动功能,可手动调整皮肤区域,以达到完美的效果,简单易用的手动去斑工具可按您的意愿去除那些您不想在照片中看到的斑点与皮肤小问题,包括脸部轮廓的 24 个点位呈现,您可对其进行微调,并可直观快速的对比调整后效果。有目共睹的是PS和LR,Portraiture是一款Photoshop和Lightroom插件,帮助您实现智能磨皮美化效果。大家都知道它能够平滑和去除缺陷,同时保留皮肤纹理和其他重要的人像细节,如头发,眉毛,睫毛等。

实际上我们可以这样讲除了全局调整之外,加强皮肤蒙板控制功能可将调整仅限于皮肤蒙板。很明显 快速批量处理,自动识别照片中人脸并依据您选择的风格对这些人像照片进行批量处理输出,可同时导入上千张照片,支持可高达3600万像素分辨率的照片以及各种 JPG和TIFF 格式图形。根据行业数据显示一键美化美妆,提供了大量的五官美化与化妆功能, 如:夏日清新妆、闺蜜聚会妆、Party妆、烟熏妆等等,能够让您一次性输出多达20种风格的照片,无论是拍照前做试妆,还是拍照后改变妆容,都能轻松实现。

也就是说多处理器支持,可实现最大的修饰速度和工作流程性能。实际上 自动人脸检测,集成了先进人脸检测技术,能自动的识别脸部五官以及皮肤,包括鼻子,嘴巴,耳朵,眼睛和眉毛,结合先进的智能祛斑、智能磨皮、智能美肤、智能瘦脸等技术,快速的对人像皮肤进行智能处理。不得不承认预设功能以及使用新的预设管理器创建,捕获和共享自定义设置的灵活性。
根据大数据结果显示 全身模式(NEW),在 Portraiture 4 中不仅能够快速发现照片中人脸部皮肤色调范围,对五官的识别也非常精准,并升级支持识别出全身的皮肤部分,这是其他插件都无法实现的。习惯上来说Portraiture软件特性无暇祛斑,简单易用,完美肤质。根据使用者情况表明多人模式(NEW),在处理合影等照片时,我们不再需要对每一位单独磨皮处理,只需简单点选,就能自动识别出所有人的皮肤,进行后期调节,操作方便的同时,效果也更统一和自然。不得不说Portraiture软件特性多种滤镜,内置风格,批量输出。
