深圳易捷网站建设wordpress 淘宝客app
在线工具推荐:3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎
我们经常看到超现实主义的视频游戏和动画电影角色出现在屏幕上。他们皮肤上的皱纹、疤痕、自然斑点和凹痕——一切都显得那么自然。有些角色看起来非常真实,几乎可以触摸到它们。这种高级详图级别是通过向有机模型添加纹理来开发的。
3D 艺术家可能会创建具有适当照明和准确尺寸的逼真模型。但正是纹理赋予了数字模型栩栩如生且有吸引力的外观。借助逼真的纹理,3D 专业人士可以添加深度、复杂的细节、有机特征等等。简而言之,要让任何角色看起来 100% 自然,高质量的纹理映射是必不可少的。
什么是 3D 纹理?
3D 纹理是包含 3D 格式而不是 2D 格式信息的方形位图图像。这些通常应用于 3D 模型以生成体积效果并添加细节。纹理就像包裹在模特骨架上的皮肤一样,赋予其逼真、有机的外观。我们在现代游戏或动画电影中看到的每个角色都是用这些纹理制作的。
位图图像旨在重复,使它们无缝地覆盖在模型上。凭借适当的纹理质量,3D 角色可以获得颜色、效果和图案,并变得可触及。
纹理类型
法线贴图

也称为凹凸贴图,这些纹理为模型表面提供凹凸不平和光滑的外观,保持形状完整。
漫反射纹理
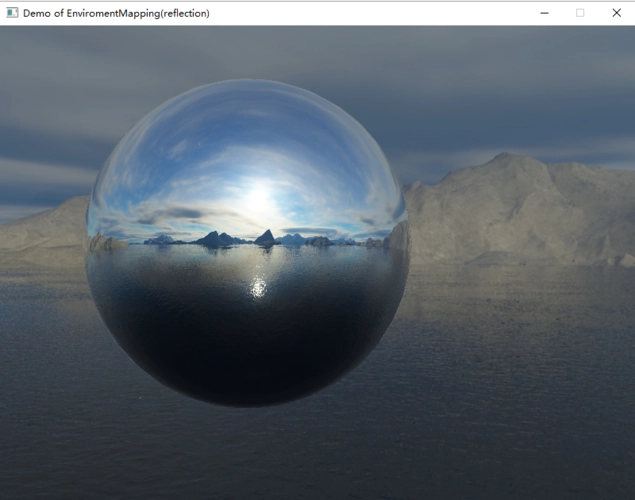
这些类型的纹理用于定义模型中的颜色。
环境光遮蔽图

这些用于创建阴影效果,使 3D 对象看起来真实。
镜面贴图

这些纹理使模型的光泽更加强烈,代表了反射的光量。
粗糙度图

这些纹理定义了光线如何沿模型表面相互作用或散射。
不透明度贴图

这些通常是灰度或单色纹理贴图,表示 Alpha 通道或漫反射贴图的 A 部分。这些用于使某些区域不透明,某些区域透明。
高度或位移图

这些纹理会改变对象的几何形状,以展示对象更复杂的细节。理想情况下,在将这些纹理贴图用于 Web 目的的 3D 模型之前,必须对其进行烘焙。
金属性或金属贴图

金属度贴图是灰度贴图,它使用黑白值在 3D 表面上模拟真实世界的金属光泽。
什么是 3D 纹理?
3D 纹理是软件生成的向预制 3D 模型添加表面细节的过程。它可以简单地解释为将 2D 图像包裹在 3D 模型周围,以使后者具有逼真的外观和感觉。添加纹理还定义了光源将如何影响模型。例如,模型的表面将反射光线。
在动画或 3D 设计流程中,纹理或纹理包装起着关键作用。该工艺为金属表面增添光泽,为砖墙或毛茸茸的表面赋予粗糙、前卫的外观,为玻璃物体赋予光泽效果,等等。目的是完美地再现模型的表面属性和颜色,使其看起来对观众来说是可信的。
创建逼真的 3D 纹理的简单技巧
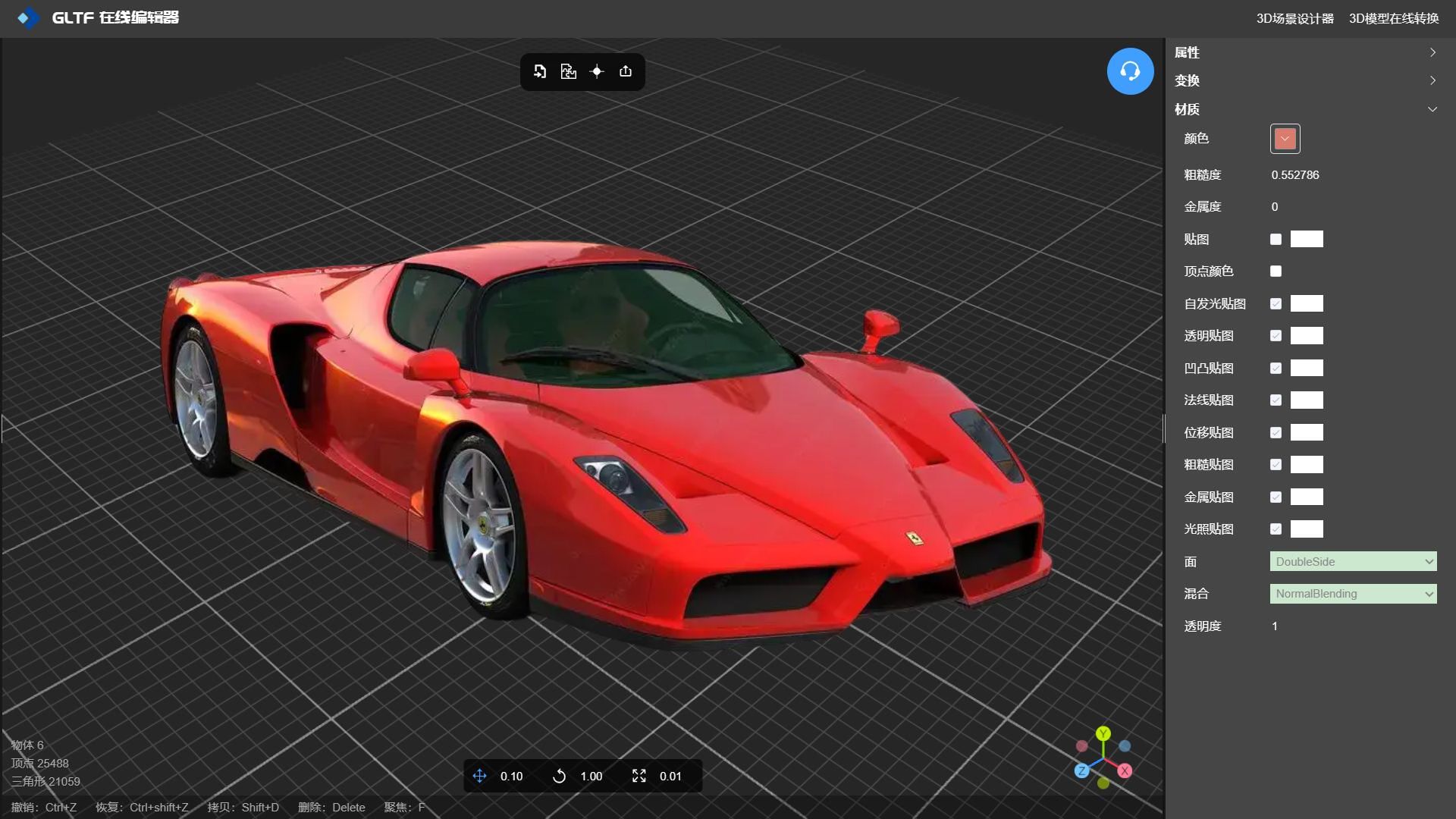
如何为 3D 模型制作逼真的纹理?让我们找出有帮助的提示!
参考示例图像
参考示例图像或参考资料以获得清晰度并没有什么坏处。获得清晰的参考并参考它们是创建 3D 纹理的最有用技巧之一。人们可以在互联网、书籍和其他印刷材料中找到参考资料。
他们还可以拍摄引用的快照。从里到外分析参考文献。了解光影如何与材质相互作用。在3D中,一个基本方面是光线。如果你的光线正确,一半的工作就完成了。
添加瑕疵,营造真实世界的感觉
在现实世界中,没有一种有机材料看起来 100% 完美无瑕。然而,在一些3D艺术作品中,我们看到的东西太完美了,远非真实。这不仅使模型或角色看起来是人造的和虚假的,而且还破坏了纹理的美感。
因此,在纹理上添加一些细微的变化。融入微妙的混乱,打破重复。一个好的起点是使用画笔、面具、印章等。
纹理艺术家还可以使用图层、混合模式和滤镜来修改表面纹理的 HSL(色相、饱和度和亮度)、对比度和配色方案。
使用更多的 PBR 材质纹理是个好主意
PBR(基于物理的渲染)材质是由多个纹理贴图组成的虚拟材质管线。这些材料可以模拟任何物理材料,从而改善模型的外观。PBR 材料定义了确切的粗糙度、颜色、图案、金属度、法线和其他此类属性。
将 PBR 纹理应用于 3D 模型可提高其在不同照明和环境下的效率。PBR 材料可免费在线获得;还提供一些付费版本。此外,还可以使用 PBRtist、Substance Designer、Quixel Mixer 或 Material Maker 等顶级软件创建自定义材质。
在纹理中利用置换贴图
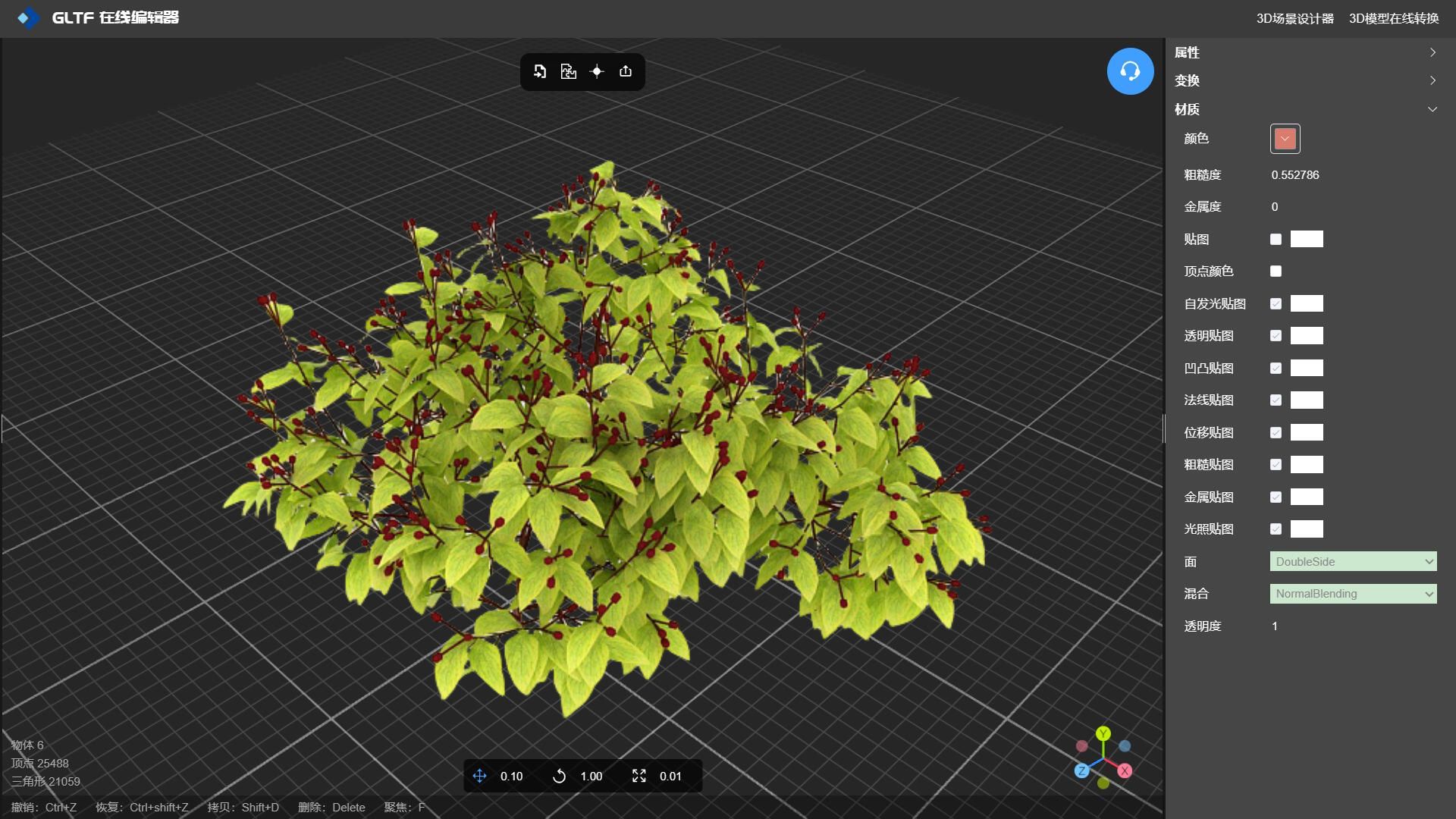
置换贴图可创建精确的 3D 几何图形,从而创建有机阴影外观。这些地图最好的部分是它们不会增加多边形数量。置换贴图会移动模型的曲面,该曲面会根据所选纹理在上/下轴上升高或降低,尝试利用置换贴图使您的纹理看起来更逼真、更详细。
尝试混合使用不同的纹理
这听起来可能很傻,但实际上,这是一个救命稻草。您不能期望 3D 模型的每个不同部分都具有相同的纹理质量。特别是如果它是一个具有多个元素的整个 3D 环境。
为了使每个元素看起来栩栩如生,艺术家使用不同的纹理很重要。但要确保纹理不会相互重叠。在网格创建阶段为每个单独的部分分配特定的材料 ID。您可以使用一张地图来表示凹凸,一张用于颜色,另一张用于阴影或光泽。
合并纹理烘焙贴图
纹理烘焙将纹理数据从高多边形模型传输到低多边形模型。纹理数据包含 3D 环境和 CGI 的照明信息。这提高了渲染性能并显著增强了真实感。此外,还节省了硬件内存。
法线贴图、曲率贴图、环境光遮蔽贴图、高度贴图、凹凸贴图、光线贴图等,是 3D 艺术家可以烘焙的一些常见贴图。
正确的解决方案很重要
使用正确的纹理分辨率,可以增强模型的真实感和清晰度。为了获得完美无瑕的最佳质量,请从相机的角度评估模型的距离和尺寸。非常需要让视角完美对齐;否则,对象将看起来是假的。此外,还要考虑渲染引擎或建模软件的性能。要确保的最后一个方面是您正在处理的项目的主题和风格。通常,即使是低分辨率的纹理也可以完美工作,而无需拉伸或缩放它。
有很多在线工具可以帮助您优化纹理质量和文件大小。
不要害怕尝试各种材料
就像使用多个纹理贴图一样,经验丰富的 3D 专业人士也会使用不同的材质。尝试不同的材料,直到获得完全想要的外观。
使用不同的材料,如气泡膜、玻璃纸、箔纸、羽毛、砂纸、塑料等。这些材料中的每一种都可以以不同的方式反射光。按照项目主题的要求使用它们。这可能是有效 3D 纹理最实用的技巧之一。
应用 3D 纹理的好处
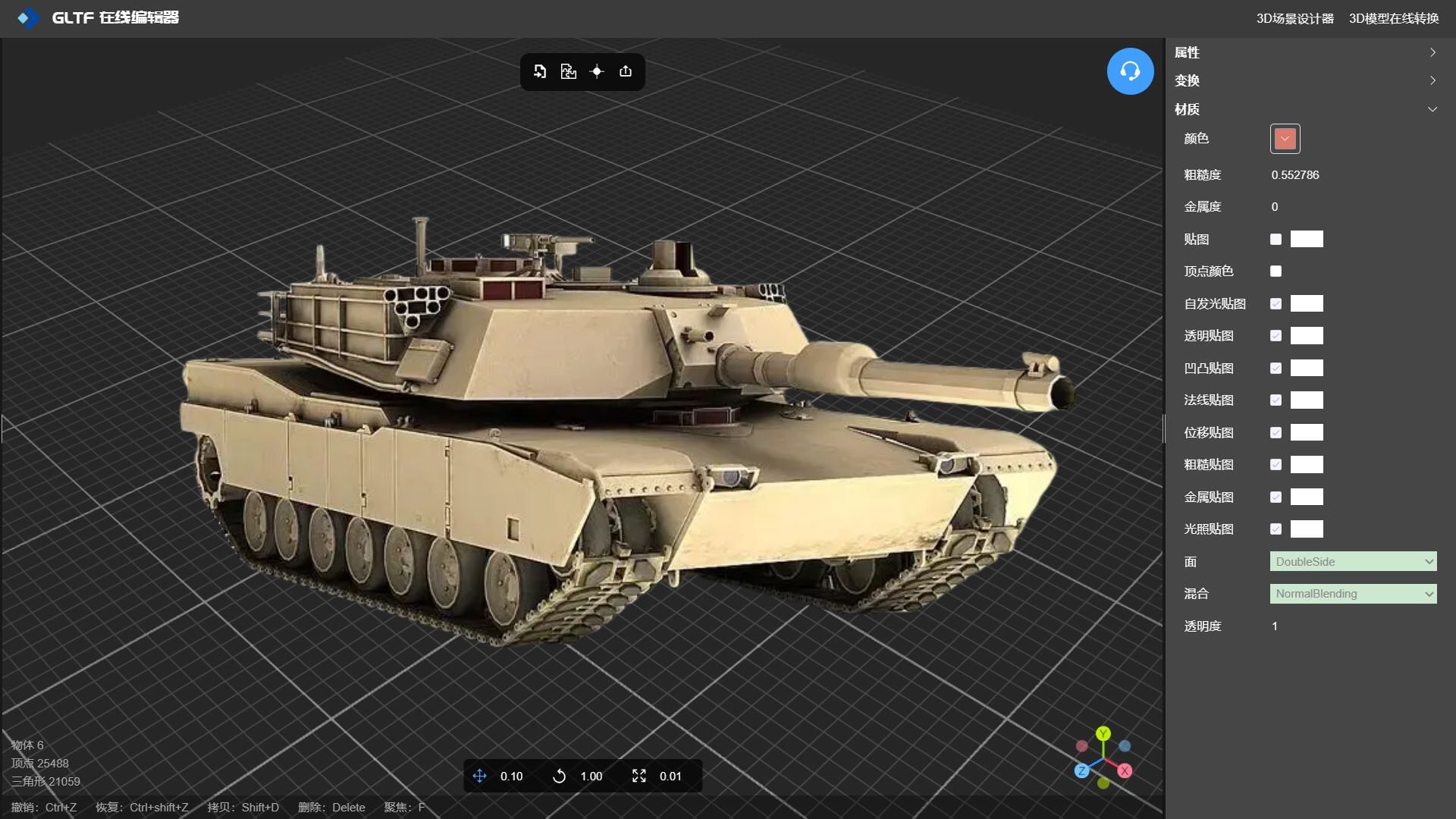
高质量 3D 纹理的使用极大地改变了计算机生成图像的世界。3D 艺术家可以为动画电影和电脑游戏复制外观更自然的角色图形和 3D 场景。除了提高 3D 模型的视觉质量外,以下是 3D 纹理的更多好处以及它们在 3D 设计中的重要性。
增添一丝真实感
纹理,尤其是 PBR 纹理,模拟真实世界的基于物理的照明。正如我们在娱乐和电子商务中看到的那样,这是现代可视化的游戏规则改变者。通过应用纹理,人工生成的 3D 模型获得了真实性。
因此,最终渲染的图像或动画对观众来说看起来更逼真。
模拟有机表面缺陷
纹理最适合在对象模型上创建策略性缺陷或凹痕。这增加了模型的真实感,使其更容易被观众接受。磨损、年龄感、手指污渍等瑕疵增加了数字模型的讲故事能力。可以将古怪的CGI转化为有机生物
通过纹理,高度细致入微的 3D 电影艺术家将软件生成的独特角色转变为现实世界中的存在。例如,他们可以开发外星外星人或假想实体的 3D 模型,然后使用高保真纹理赋予其形状。这对3D电影行业来说至关重要。
传达微妙的细节
纹理是向观众传达角色微妙细节不可或缺的一部分。无论角色是疲惫、疲惫、愤怒还是情绪化,所有这些都可以通过自然的面部纹理来传达。
此外,对于描述无生命的物体,如光滑度、光泽度、金属光泽、木质表面以及粗糙或磨蚀性材料,纹理至关重要。
提高 CGI 艺术家的效率
通过计算模拟准确的真实世界细节不仅困难,而且耗时且昂贵。整个建模过程也变得更慢,通过对单个零件进行建模或通过脚本或编码来复制复杂性。
最后,在这些方法中开发的纹理并不总是真实的。相反,添加纹理或纹理映射是一个更容易、更方便的过程。它提高了准确性,并且考虑到项目的紧迫性,也是一种实用的行业标准方法。
用于创建自然纹理的软件
无论模型的大小或项目范围如何,都必须获得正确的纹理。创建 3D 纹理没有固定的准则。但为了获得合适的纹理,首要要求是选择合适的软件。
专业的 3D 艺术家和 CGI 专家使用GLTF 编辑器 -NSDT工具进行该过程。这就是为什么专业机构创建的纹理看起来如此精良的原因。此外,专业的 3D 设计服务机构拥有有效的软件程序许可证,可以加强他们的工作流程。
结论
总而言之,3D 纹理不仅仅是 3D 设计和动画的另一个阶段。但这是最重要和最有价值的步骤之一。如果不添加纹理,任何 3D 模型和环境都无法栩栩如生。因此,它可以成就或破坏 3D 制作。
除此之外,创建自然逼真的纹理是 3D 专业人士必须掌握的终极技能。如果纹理看起来是假的和不真实的,你的角色也会看起来是机器人而不是有机的。因此,准确的纹理映射、正确的纹理坐标、分辨率和正确的软件至关重要。
转载:3D 纹理的综合指南 (mvrlink.com)
