有时候把Label的AutoSize属性设置为True,当窗体显示的时候,Label中的内容可能会显示不完全,只能把AutoSize设置为False,
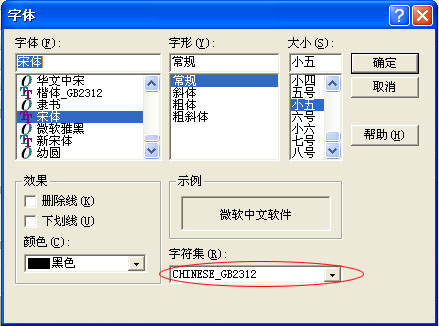
把Label调整成能显示出内容的大小。还有一种更简单的解决方法。把Form的Font属性进行如下设置:字体为宋体,字号为小五,
字形为常规,字符集为“CHINESE_GB2312”,把Label的ParentFont设置为True即可!

有时候把Label的AutoSize属性设置为True,当窗体显示的时候,Label中的内容可能会显示不完全,只能把AutoSize设置为False,
把Label调整成能显示出内容的大小。还有一种更简单的解决方法。把Form的Font属性进行如下设置:字体为宋体,字号为小五,
字形为常规,字符集为“CHINESE_GB2312”,把Label的ParentFont设置为True即可!
转载于:https://www.cnblogs.com/huhu0013/archive/2010/07/12/1775449.html