正规网站制作公司有哪些想自己做一个网站
介绍
蓝牙技术是一种无线数据和语音通信开放的全球规范,它是基于低成本的近距离无线连接,为固定和移动设备建立通信环境的一种特殊的近距离无线技术连接。本示例通过@ohos.bluetooth 接口实现蓝牙设备发现、配对、取消配对功能。实现效果如下:
效果预览
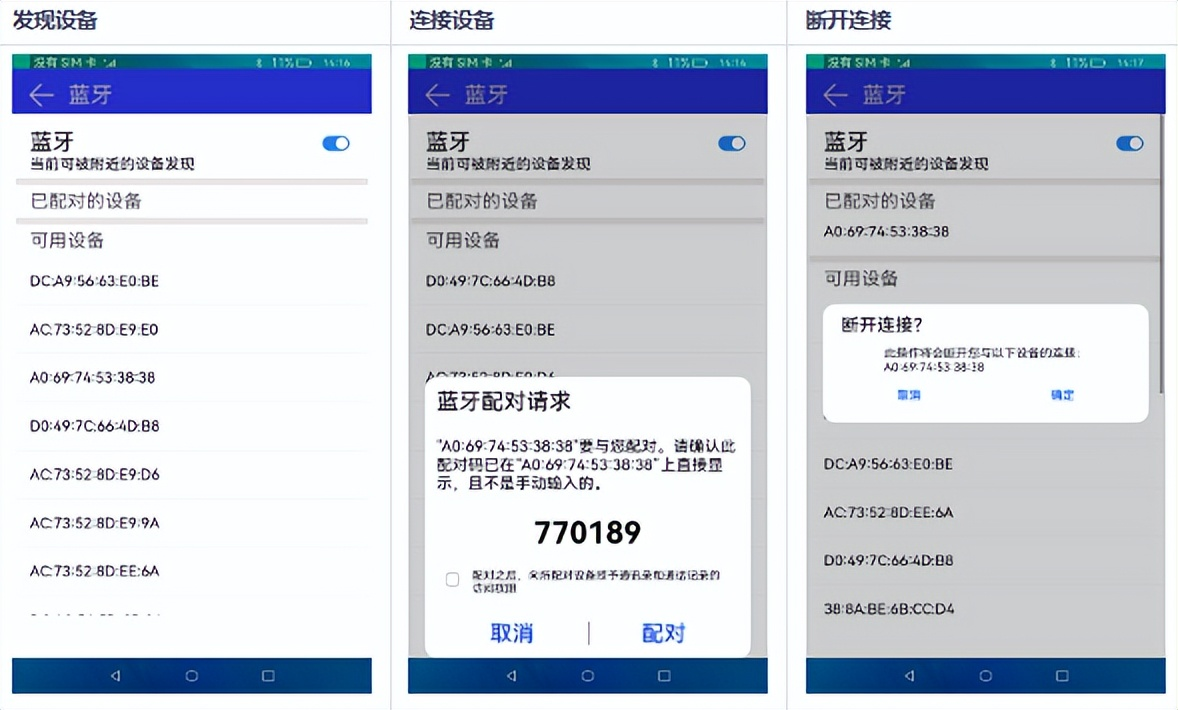
使用说明
1.启动应用,若蓝牙本来就打开的,系统会直接搜索周围可配对的设备,若蓝牙未打开,打开开关。
2.搜索到附近的设备后,选择需要配对的设备,点击该设备,会跳出匹配弹窗,若确定匹配,点击匹配按钮,否则点击取消按钮。
3.匹配后,若想删除匹配的设备,点击已配对的设备列表中的设备,会跳出断开连接弹窗,若确定删除该设备,点击确定,否则点击取消。
工程目录
entry/src/main/ets/
|---Application
|---Common
| |---PinDialog.ets // 任务信息组件
| |---TitleBar.ets // 标题组件
|---MainAbility
|---Model
| |---Logger.ts // 日志工具
|---pages
| |---Index.ets // 首页
具体实现
- 蓝牙设备发现、配对、取消配对等操作的功能结构主要封装在Index、PinDialog
- 启动和关闭蓝牙:在Index页面中通过Toggle组件的onChange函数来控制蓝牙的开关,开关打开的情况下会执行initBluetooth函数,关闭的情况下执行bluetooth.disableBluetooth()方法来断开蓝牙;
- 验证蓝牙是否处于连接状态:蓝牙打开的时候通过bluetooth.on(‘stateChange’)方法来监听蓝牙连接状态改变事件,确认已打开,则执行foundDevices()函数来查找设备接口,确认已关闭则执行bluetooth.stopBluetoothDiscovery()方法来停止查询接口。
- 发现设备:在foundDevices()函数中通过bluetooth.on(‘bluetoothDeviceFind’)方法来监听设备发现事件,并且通过bluetooth.getPairedDevices()方法来更新已配对蓝牙地址,然后通过bluetooth.startBluetoothDiscovery()方法开启蓝牙扫描,去发现远端设备,并且通过bluetooth.setBluetoothScanMode()方法来被远端设备发现。
- 蓝牙配对:通过bluetooth.on(‘pinRequired’)方法来监听远端蓝牙设备的配对请求事件,点击配对执行bluetooth.setDevicePairingConfirmation(this.data.deviceId,true)方法,点击取消执行bluetooth.setDevicePairingConfirmation(this.data.deviceId,false)方法。
- 取消配对:最后通过bluetooth.cancelPairedDevice()来断开指定的远端设备连接。
相关权限
ohos.permission.USE_BLUETOOTH
ohos.permission.LOCATION
ohos.permission.DISCOVER_BLUETOOTH
ohos.permission.MANAGE_BLUETOOTH
ohos.permission.APPROXIMATELY_LOCATION
依赖
不涉及。
约束与限制
1.本示例仅支持标准系统上运行。
2.本示例已适配API version 9版本SDK,本示例涉及使用系统接口:cancelPairedDevice(),需要手动替换Full SDK才能编译通过。
3.本示例需要使用DevEco Studio 3.1 Beta2 (Build Version: 3.1.0.400, built on April 7, 2023)及以上版本才可编译运行。
4.本示例所配置的权限ohos.permission.MANAGE_BLUETOOTH为system_basic级别(相关权限级别可通过权限定义列表 查看),需要手动配置对应级别的权限签名(具体操作可查看自动化签名方案) 。
下载
如需单独下载本工程,执行如下命令:
git init
git config core.sparsecheckout true
echo code/SystemFeature/Connectivity/Bluetooth/ > .git/info/sparse-checkout
git remote add origin https://gitee.com/openharmony/applications_app_samples.git
git pull origin master
为了帮助大家更深入有效的学习到鸿蒙开发知识点,小编特意给大家准备了一份全套最新版的HarmonyOS NEXT学习资源,获取完整版方式请点击→HarmonyOS教学视频:https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
HarmonyOS教学视频:语法ArkTS、TypeScript、ArkUI等…视频教程


鸿蒙生态应用开发白皮书V2.0PDF: 获取完整版白皮书方式请点击→https://docs.qq.com/doc/DZVVkRGRUd3pHSnFG?u=a42c4946d1514235863bb82a7b2ac128

鸿蒙 (Harmony OS)开发学习手册→https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
一、入门必看
1.应用开发导读(ArkTS)
2………
二、HarmonyOS 概念→https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
1.系统定义
2.技术架构
3.技术特性
4.系统安全
5…

三、如何快速入门?→https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
1.基本概念
2.构建第一个ArkTS应用
3…

四、开发基础知识→https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
1.应用基础知识
2.配置文件
3.应用数据管理
4.应用安全管理
5.应用隐私保护
6.三方应用调用管控机制
7.资源分类与访问
8.学习ArkTS语言
五、基于ArkTS 开发→https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
1.Ability开发
2.UI开发
3.公共事件与通知
4.窗口管理
5.媒体
6.安全
7.网络与链接
8.电话服务
9.数据管理
10.后台任务(Background Task)管理
11.设备管理
12.设备使用信息统计
13.DFX
14.国际化开发
15.折叠屏系列
更多了解更多鸿蒙开发的相关知识可以参考:https://docs.qq.com/doc/DZVVBYlhuRkZQZlB3
