英文网站seo发展前景中信建设有限责任公司深圳中信金融中心项目工期专业招标
大家好,今天给大家分享的是一个基于Spring Boot开发的开源项目,旨在提供一个功能强大的基于Docker的本地托管PDF操作工具Stirling PDF。

项目介绍
Stirling-PDF是一个全面的PDF工具箱,适用于个人和企业用户,尤其对于那些重视数据隐私和需要在本地环境中处理敏感文档的场景非常适用。
系统功能
- 深色模式支持。
- 自定义下载选项
- 并行文件处理和下载
- 用于与外部脚本集成的 API
- 可选的登录和身份验证支持
- 数据库备份和导入
PDF处理功能
页面操作
-
查看和修改 PDF - 通过自定义查看排序和搜索查看多页 PDF。加上页面编辑功能,如注释、绘图以及添加文本和图像。 (使用 PDF.js 和 Joxit 和 Liberation.Liberation 字体)
-
用于合并/分割/旋转/移动 PDF 及其页面的完整交互式 GUI。
-
将多个 PDF 合并为一个结果文件。
-
将 PDF 拆分为指定页码的多个文件,或将所有页面提取为单独的文件。
-
将 PDF 页面重新组织为不同的顺序。
-
以 90 度增量旋转 PDF。
-
删除页面。
-
多页布局(将 PDF 设置为多页页面)。
-
按设定的百分比缩放页面内容大小。
-
调整对比度。
-
裁剪 PDF。
-
自动分割 PDF(使用物理扫描的页面分隔符)。
-
提取页面。
-
将 PDF 转换为单页。
转换操作
-
将 PDF 与图像相互转换。
-
将任何常见文件转换为 PDF(使用 LibreOffice)。
-
将 PDF 转换为 Word/Powerpoint/其他(使用 LibreOffice)。
-
将 HTML 转换为 PDF。
-
将URL地址转换为 PDF。
-
将Markdown内容转换为 PDF。
安全与权限
-
添加和删除密码。
-
更改/设置 PDF 权限。
-
添加水印。
-
认证/签署 PDF。
-
清理 PDF。
-
自动删除文本。
其他
- 添加/生成/写入签名。
- 修复 PDF。
- 检测并删除空白页。
- 比较 2 个 PDF 并显示文本差异。
- 将图像添加到 PDF。
- 压缩 PDF 以减小文件大小(使用 OCRMyPDF)。
- 从 PDF 中提取图像。
- 从扫描中提取图像。
- 添加页码。
- 通过检测 PDF 标题文本自动重命名文件。
- PDF 上的 OCR(使用 OCRMyPDF)。
- PDF/A 转换(使用 OCRMyPDF)。
- 编辑元数据。
- 拼合 PDF。
- 获取 PDF 上的所有信息以查看或导出为 JSON。
采用技术栈
- Spring Boot + Thymeleaf
- PDFBox
- 高级转换功能使用LibreOffice实现
- OcrMyPdf
- HTML, CSS, JavaScript
- Docker
- PDF.js
- PDF-LIB.js
安装使用
安装
Stirling PDF 有 3 个不同的版本:完整版本、超精简版以及“胖”版本。根据您使用的功能类型,您可能需要较小的图像以节省空间。对于不介意空间优化的人,只需使用最新的标签。
请注意,在下面的示例中,您可能需要根据需要更改卷路径,当前示例将它们安装到当前工作目录,例如 ./extraConfigs:/configs 到 /opt/stirlingpdf/extraConfigs:/configs
Docker Run
docker run -d \-p 8080:8080 \-v ./trainingData:/usr/share/tessdata \-v ./extraConfigs:/configs \-v ./logs:/logs \-e DOCKER_ENABLE_SECURITY=false \-e INSTALL_BOOK_AND_ADVANCED_HTML_OPS=false \-e LANGS=en_GB \--name stirling-pdf \frooodle/s-pdf:latest也可以添加这些进行定制,但不是必需的-v /location/of/customFiles:/customFiles \Docker Compose
version: '3.3'
services:stirling-pdf:image: frooodle/s-pdf:latestports:- '8080:8080'volumes:- ./trainingData:/usr/share/tessdata #Required for extra OCR languages- ./extraConfigs:/configs
# - ./customFiles:/customFiles/
# - ./logs:/logs/environment:- DOCKER_ENABLE_SECURITY=false- INSTALL_BOOK_AND_ADVANCED_HTML_OPS=false- LANGS=en_GB如果你想支持OCR相关功能,请阅读如何集成ORC功能。
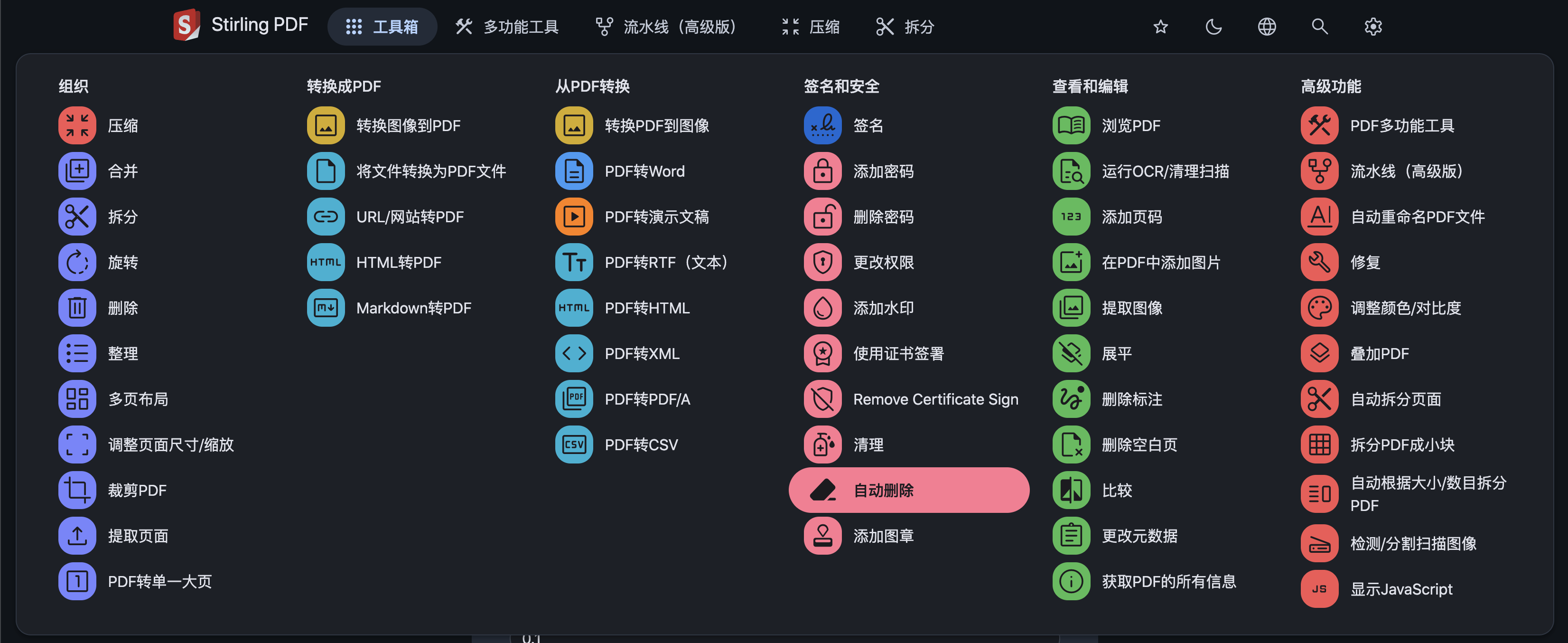
使用截图
URL转PDF

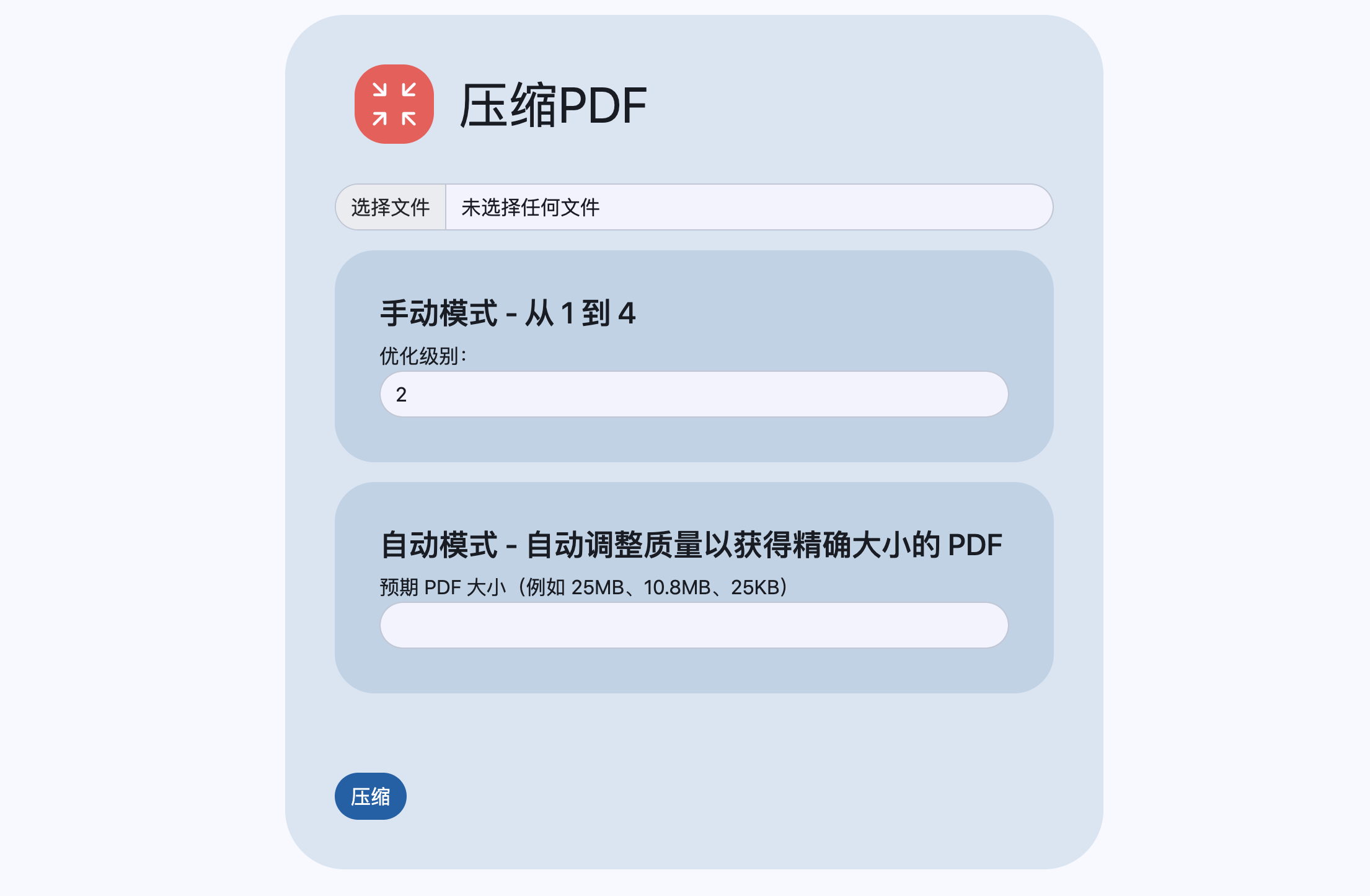
压缩PDF
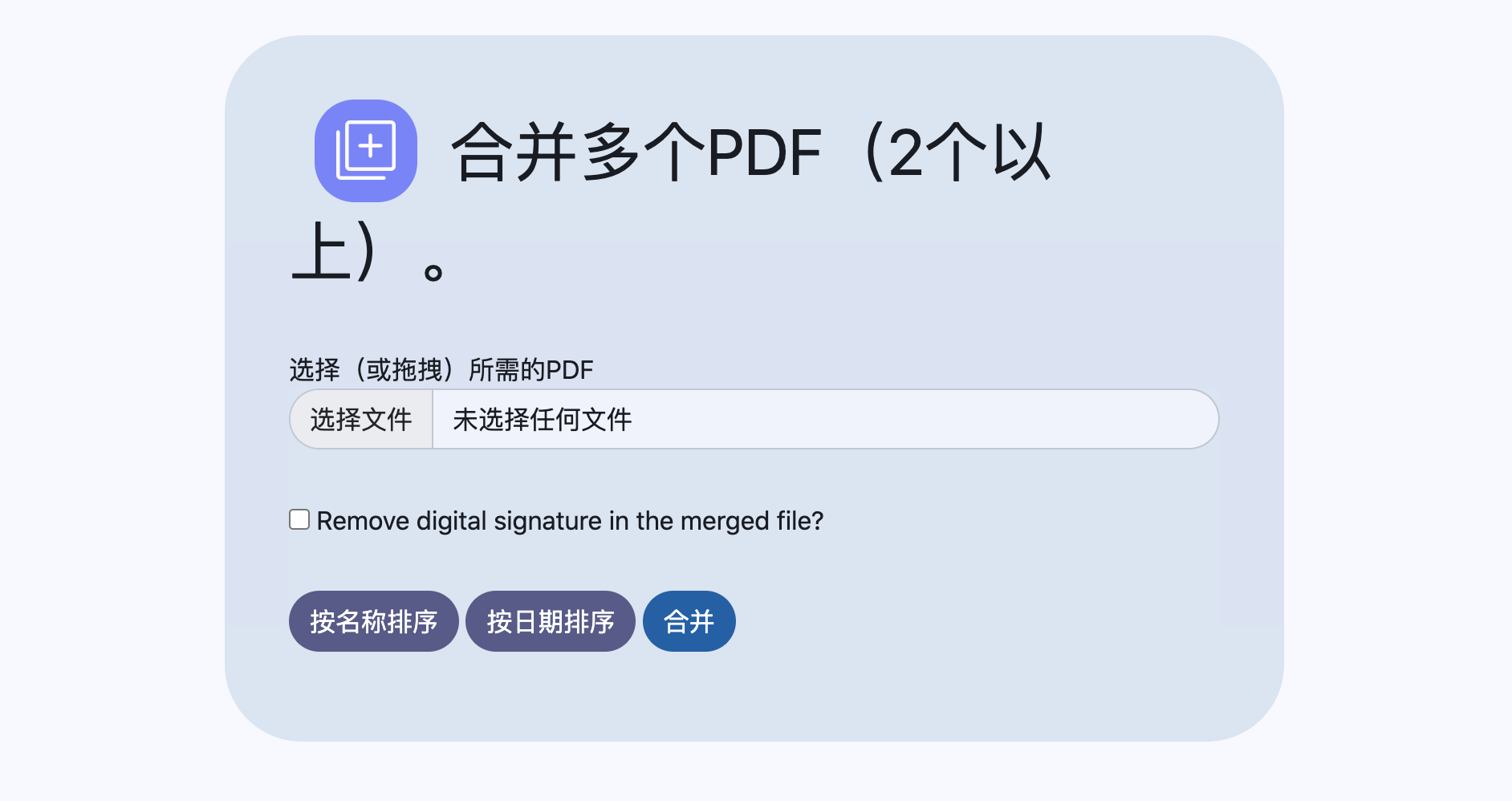
合并PDF
PDF转Word

PDF添加水印

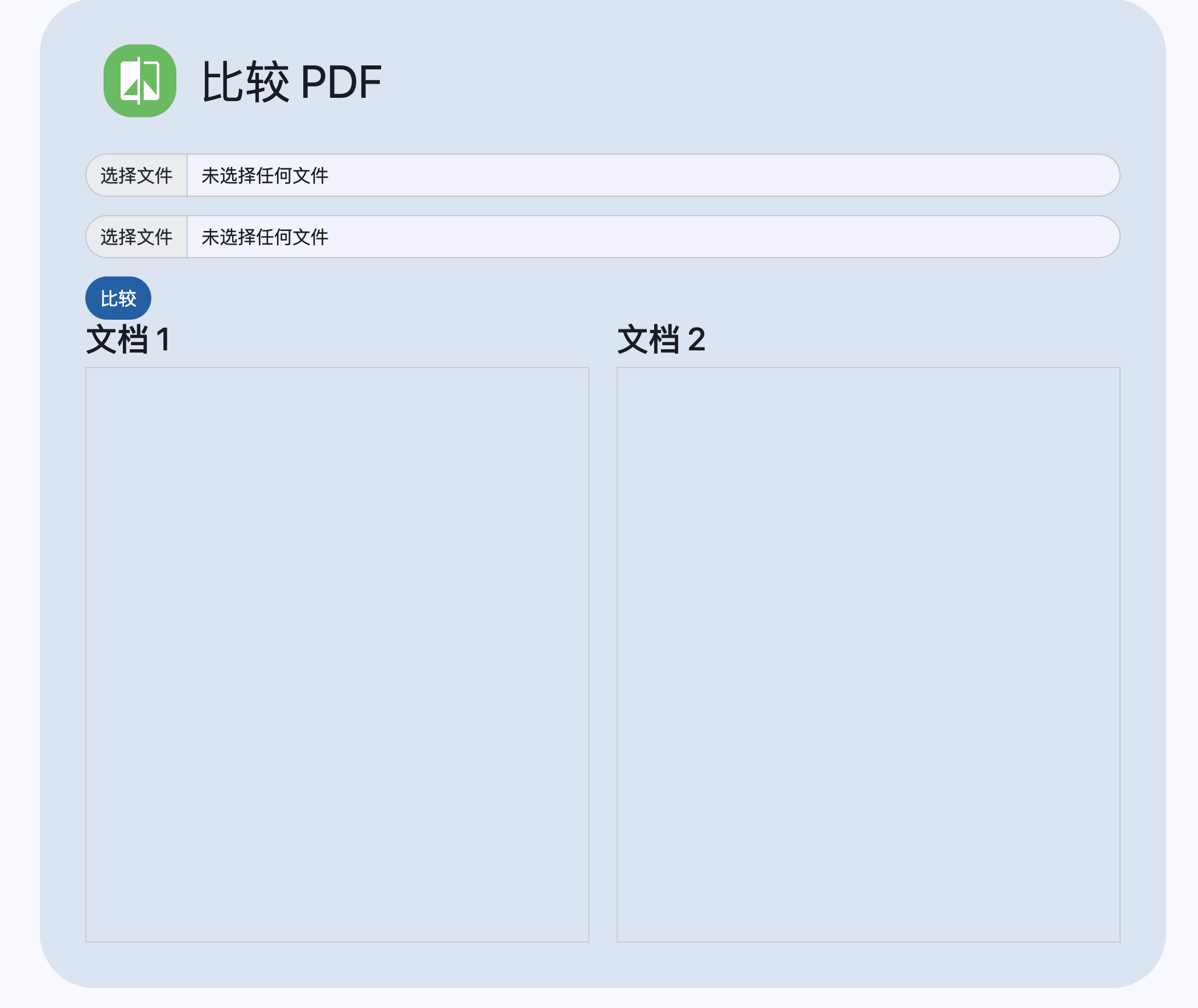
比较PDF
项目地址
https://github.com/Stirling-Tools/Stirling-PDF一款允许使用Docker部署本地托管的、基于 Web 的 PDF 操作工具 - BTool博客 - 在线工具软件,为开发者提供方便
