百度收录网站入口鹤壁市城乡一体化示范区范围
查看提示
先看png图片

发现最左侧有些信息
看了大佬们的wp,需要写脚本把左侧这块读出来,黑色对应1,白色对应0,再转成字符
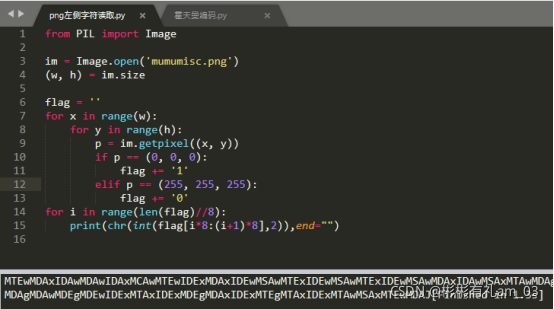
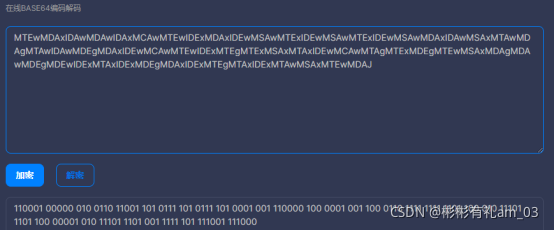
得到的结果base64解码,得到:
回过头看private.key,它其实是个jpg图片,改后缀,得到

结合提示,得知这个是霍夫曼树,前面得到的那个应该就是霍夫曼编码了,写脚本

得到flag
查看提示
先看png图片

发现最左侧有些信息
看了大佬们的wp,需要写脚本把左侧这块读出来,黑色对应1,白色对应0,再转成字符

得到的结果base64解码,得到:

回过头看private.key,它其实是个jpg图片,改后缀,得到

结合提示,得知这个是霍夫曼树,前面得到的那个应该就是霍夫曼编码了,写脚本

得到flag